Неизвестный танк часть 5
- Опубликовано: 23.04.2016, 13:59
- Просмотров: 120902
Содержание материала
Неизвестный танк...
(Раздел создан на основании книги "Танк" Военного издательства Министерства Обороны СССР 1954 года, под редакцией
Антонова А.С., Артамонова Б.А., Коробкова Б.М., Магидович Е.И. и других материалах.)
Часть 5
ГЛАВА ДЕВЯТАЯ
ПОВОРОТЛИВОСТЬ
Одно из важнейших боевых свойств, определяющих маневренность танка, — его поворотливость. От поворотливости в большой степени зависит средняя скорость танка, а также его неуязвимость и огневая мощь. Чем поворотливее танк, тем меньше возможность пора жения его огнем противника и тем лучше можно использовать его огневые средства. Хорошая поворотливость обеспечивает возможность танку маневрировать в наиболее сложных условиях боя; в случае преодоления укрепленных полос, при действиях в горах, в населенных пунктах.
Поворотливость оценивается угловой скоростью поворота, т, е. углом, на который танк может повернуться в единицу времени (в секунду), и наименьшим радиусом поворота. От угловой скорости зависит быстрота поворота; наименьший радиус характеризует способность танка менять курс своего движения в узких проходах. Поворотливость гусеничной машины гораздо выше поворотливости колесной именно потому, что минимальный радиус поворота гусеничной машины во много раз меньше минимального радиуса поворота колесной машины. Поэтому танки могут маневрировать там, где не могут маневрировать автомобили (например, в лесу). В этом смысле от поворотливости зависит и проходимость танка.
В настоящей главе рассматриваются условия поворота танка, силы, действующие на него при повороте, и особенности передачи мощности при повороте. Рассмотрение этих вопросов позволяет выяснить, каким требованиям должны удовлетворять механизмы поворота танка, и сравнить различные механизмы.
ПОВОРОТ ТАНКА
РАДИУС ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
Для поворота тапка нужно, чтобы его ведущие колеса вращались с разным числом оборотов, В этом случае с разной скоростью будут двигаться и гусеницы. Гусеница, имеющая при повороте большую скорость, называется забегающей, меньшую — отстающей. Танк поворачивается в сторону отстающей гусеницы.
Крутизна поворота танка определяется радиусам окружности, которую описывает точка, лежащая на пересечении продольной и поперечной осей опорной поверхности забегающей гусеницы. Этот радиус называется радиусом поворота танка, а центр окружности — центром поворота.
Радиус поворота зависит от соотношения скоростей забегающей и отстающей гусениц. При вращении гусениц в одну и ту же сторону танк будет поворачиваться тем круче, чем меньше скорость отстающей гусеницы по сравнению со скоростью забегающей.
Наименьший возможный для гусеничной машины радиус поворота получается при вращении гусениц в разные стороны с одинаковой скоростью. В этом случае центр поворота находится между гусеницами на равном расстоянии от каждой из них, а радиус поворота равен половинеширины колеи танка R= B/2 (рис. 469.А).
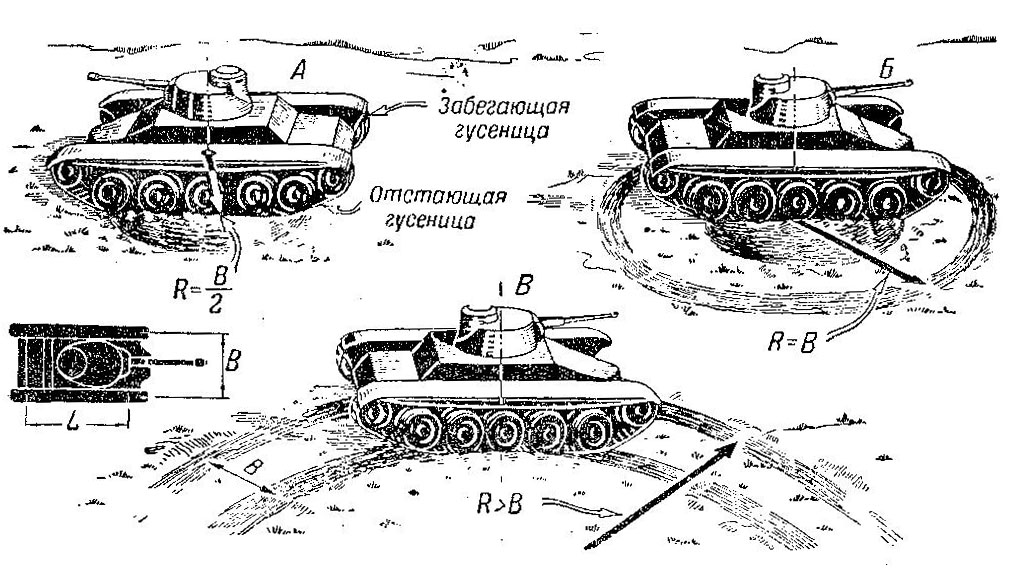
Рис. 469. Различные радиусы поворота танка
Если отстающая гусеница неподвижна, танк поворачивается вокруг нее; тогда радиус поворота равен ширине колеи В (рис. 469,Б). Наконец, если отстающая гусеница вращается в ту же сторожу, что и забегающая, радиус поворота больше ширины колеи (рис. 469, В). При равных скоростях обеих гусениц танк движется прямо.
Каждый танк имеет свой наименьший радиус поворота, величина которого зависит от устройства механизмов поворота. Как уже указывалось, наименьший радиус характеризует способность танка маневрировать в узких проходах.
На рис. 470 показаны три танка, имеющих разные наименьшие радиусы поворота.

Рис. 470. Чем меньший радиус поворота может иметь танк, тем он поворотливее
Различна и их поворотливость. Если танк, изображенный в верхней части рисунка, может повернуться на 90° с нескольких заездов, то танк, показанный посередине, имеющий меньший радиус поворота, должен предварительно принять вправо и потом уже двигаться по нужному ему курсу; танк, показанный в нижней части рисунка, может по вернуться с одного заезда.
У большинства танков наименьший радиус поворота теоретически равен ширине колеи В. При этом предполагается, что отстающая гусеница полностью заторможена и скорость ее равна нулю (рис. 471.А).
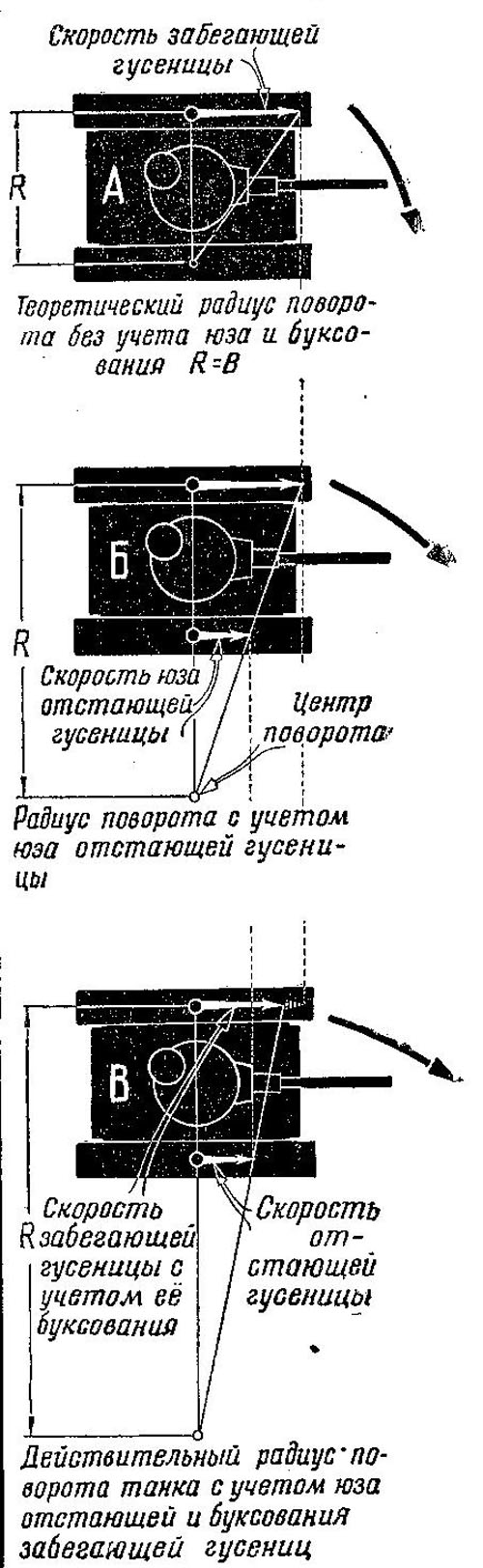
Рис. 471. Влияние буксования и юза гусениц на радиус поворота танка
В действительности это неосуществимо. При полностью затянутом тормозе отстающая гусеница движется юзом, т. е, ее опорная ветвь не лежит на грунте неподвижно, а проскальзывает вперед, в сторону движения танка. Поэтому центр поворота танка находится не под серединой отстающей гусеницы, а смещен за ее наружный край, как это показано на рис. 471.Б. Действительный радиус поворота будет поэтому больше ширины колеи. Иногда действительный радиус больше теоретического на 30—50%, т. е. наименьший радиус равен 1,3—1,5 В. Если тормоз затянут не полностью, действительный радиус поворота оказывается больше теоретического не только вследствие юза заторможенной гусеницы. На радиус поворота оказывает влияние еще и буксование забегающей гусеницы. Опорная ветвь этой гусеницы смещается (сползает) назад, в силу чего уменьшается скорость гусеницы. Как это влияет на величину радиуса поворота, можно понять из рис. 471,В.
Итак, мы рассмотрели первую величину, характеризующую поворотливость танка, — его радиус поворота.
Вторая величина, определяющая поворотливость танка,— это угловая скорость поворота. На рис. 472 танк, показанный слева, поворачивается за одно и то же время на больший угол, чем танк, показанный справа, т. е. угловая скорость первого танка выше, чем второго.
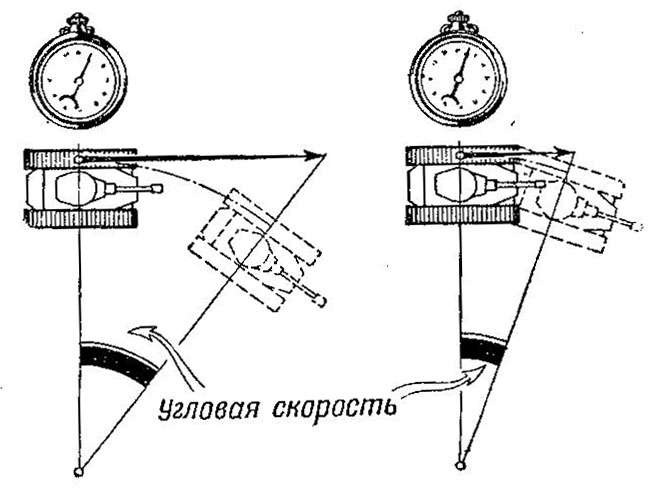
Рис. 472. Различные угловые скорости поворота танка
Для того чтобы правый танк повернулся на такой же угол, как и левый танк, потребуется больше времени. Следовательно, поворотливость правого танка хуже.
Наибольшая угловая скорость танка равна 45—60° в секунду. Это значит, что на 90° танк может повернуться за 1,5—2 секунды, а изменить курс движения на обратный путем разворота на 180° за 3—4 секунды.
Особенно валико значение угловой скорости поворота для самоходно-артиллерийских установок, так как у них маневр огнем обеспечивается только маневром гусеницами, т. е. поворотливостью.
Из рис. 471 нетрудно установить, что буксование забегающей и юз отстающей гусениц при повороте не только увеличивают радиус, но и уменьшают угловуюскорость поворота.
КАК ПРОИСХОДИТ ПОВОРОТ
РАВНОМЕРНЫЙ И НЕРАВНОМЕРНЫЙ ПОВОРОТ
В главе VIIIбыло показано, что при равномерном прямолинейном движении танка сила тяги должна равняться силе сопротивления движению. В этом случае танк движется с постоянной скоростью, которую он приобрел в период разгона.
При повороте движение танка определяется скоростями обеих гусениц — забегающей и отстающей. Если скорость гусениц условно изобразить стрелками, как это показано на рис, 473, и приложить эти стрелки к серединам гусениц, то графически легко представить, как происходит поворот танка.
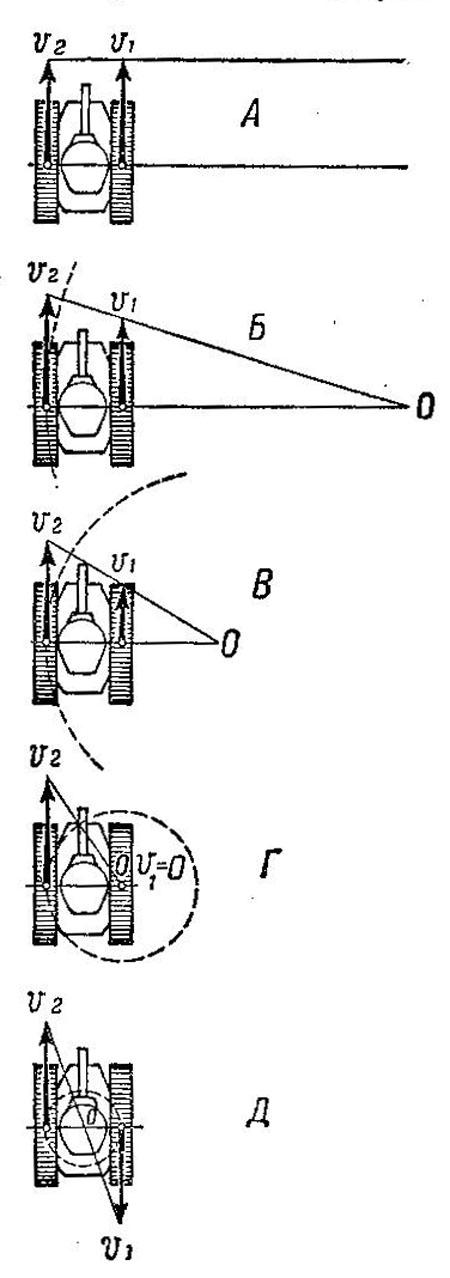
Рис. 473. Зависимость радиуса поворота танка от скорости отстающей гусеницы
При скоростях v2 = v1 (рис. 473, А) танк движется прямолинейно. При уменьшении скорости отстающей гусеницы (рис. 473, Б и В) центр поворота (точка O) приближается к танку, танк поворачивается со все уменьшающимся радиусом. Если полностью затормозить отстающую гусеницу (рис. 473,Г), танк будет поворачиваться вокруг заторможенной гусеницы, причем радиус поворота будет равен ширине колеи танка В (юз не учитывается). При вращении гусениц в разные стороны (рис. 473, Д) радиус поворота равен половине ширины колеи B/2.
Допустим, что движущийся танк должен начать поворот. Для этого отъединяют от-стающую гусеницу и тормозят ее. Полагаем, что при этом скорость забегающей гусеницы (v2) не меняется. По мере притормаживания отстающей гусеницы радиус поворота танка постепенно уменьшается. Если скорость v2 остается постоянной, то с уменьшением радиуса поворота угловая скорость танка увеличивается. Наибольшая угловая скорость будет при повороте с радиусом B/2(рис. 473, Д).
При прямолинейном движении скорость движения танка изменяется только в том случае, когда сила тяги больше или меньше силы сопротивления движению. Если сила тяги больше силы сопротивления, скорость танка увеличивается, если меньше -уменьшается. Когда сила тяги равна силе сопротивления, танк движется равномерно. Подобное же явление происходит при повороте; так как танк поворачивается под действием пары сил, то, если момент этой пары больше момента сопротивления (см. ниже), угловая скорость поворота увеличивается. Сильнее притормаживая отстающую гусеницу и увеличивая поворачивающий момент, снижают скорость гусеницы и тем самым уменьшают радиус поворота и увеличивают угловую скорость поворота танка. При изменении радиуса поворота танк поворачивается не по окружности, а по закручивающейся спирали (рис. 474).

Рис. 474. Неравномерный поворот по спирали с переменным радиусом
Такой поворот называется неравномерным. При неравномерном повороте центр поворота не остается на месте, как при равномерном повороте с Постоянными скоростями и постоянными радиусами (рис. 475), а перемещается, как и танк, по закручивающейся спирали.
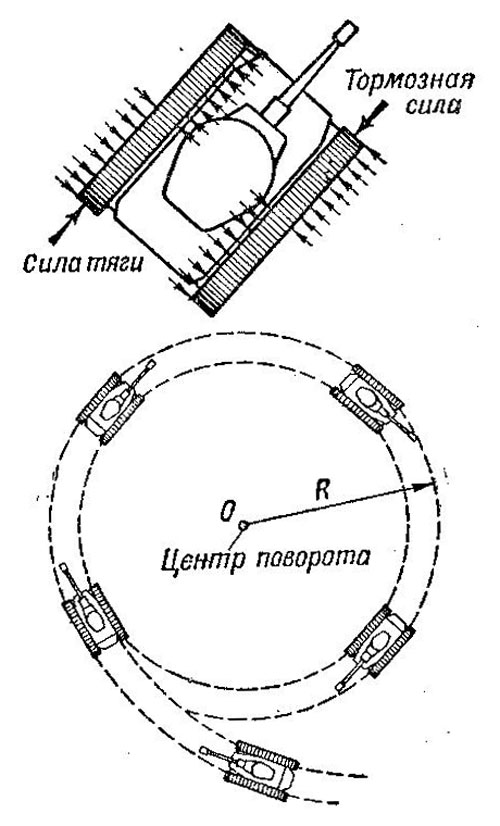
Рис. 475. Равномерный поворот по окружности с постоянным радиусом
Если уменьшить торможение отстающей гусеницы, ее скорость возрастет, и радиус поворота увеличится. Танк будет двигаться по раскручивающейся опирали. Если совеем перестать притормаживать отстающую гусеницу, ее скорость увеличится настолько, что танк станет двигаться почти прямолинейно.
Практически равномерный поворот совершается редко, так как трудно допустить, что силы и пары сил, поворачивающие танк, в точности равны силам и парам, сопротивляющимся его повороту. Как пра-вило, танк поворачивается неравномерно, и только для удобства рассмотрения явлений, происходящих при повороте, допускают, что поворот происходит равномерно, т. е, по окружности, и с постоянной скоростью.
СИЛА ИНЕРЦИИ ПРИ ПОВОРОТЕ
Если скорость танка перед началом поворота достаточно велика, поворот значительно облегчается благодаря силе инерции прямолинейного движения. Эта сила появляется в момент торможения отстающей гусеницы вследствие уменьшения скорости танка. Сила инерции приложена к центру тяжести танка и направлена в сторону движения танка (рис. 476).
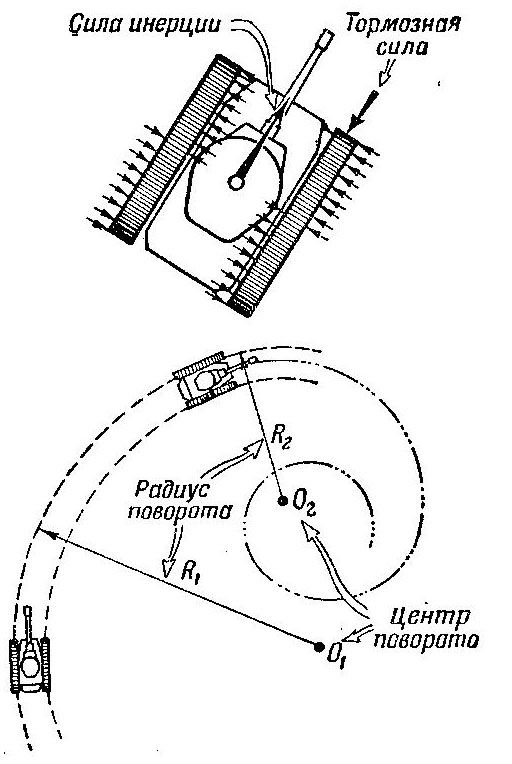
Рис. 476. Сила инерции при повороте
Сила инерции может быть использована как поворачивающая сила, когда на забегающей гусенице нельзя создать силу тяги. Если одна из гусениц сбита в бою, танк все же можно вывести из-под огня противника, используя оставшуюся гусеницу. При уводе танка в сторону его «выравнивают», резко притормаживая гусеницу.
Величина силы инерции зависит от резкости торможения. Чем резче затормозить гусеницу, тем больше будет сила инерции. Продолжительность действия силы инерции зави-сит от величины живой силы танка,
которая тем больше, чем выше скорость танка; поэтому силу инерции используют на высших передачах, быстро затягивая тормоз на короткое время и обеспечивая таким образом поворот на небольшой угол.
с двухступенчатым планетарным механизмом поворота имеет два устойчивых радиуса поворота; танк с электротрансмиссией не имеет ни одного устойчивого радиуса, поэтому там требуется постоянно регулировать поворот.
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ТАНК ПРИ ПОВОРОТЕ
При прямолинейном движении танка силы тяги, приложенные к обеим гусеницам, направлены вперед. При повороте же танка нужно» чтобы эти силы были направлены в противоположные стороны, т. е. необходимо создать на забегающей гусенице силу тяги, направленную вперед, а на отстающей — тормозную силу, направленную назад (рис, 477).
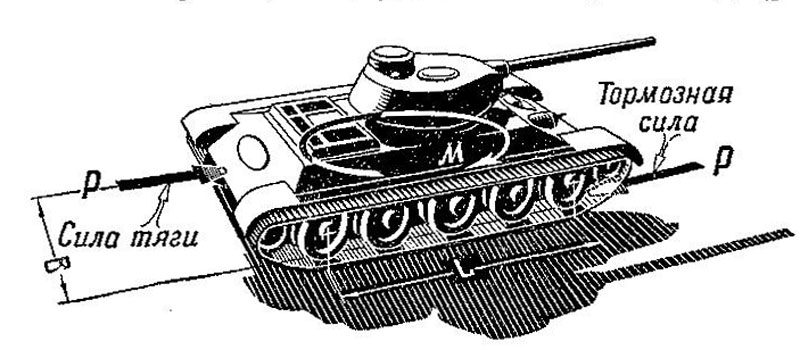
Рис. 477. Сила тяги и тормозная сила создают пару сил,поворачивающую танк
Другими словами. для осуществления поворота танка необходимо приложить к нему пару сил. Расстояние между силами (плечо пары) равно ширине колеи танка В; поэтому момент пары М. поворачивающей танк, равен
M = PB
СОПРОТИВЛЕНИЕ ПОВОРОТУ
Пара сил, создаваемая на гусеницах, необходима для преодоления сопротивления повороту. Характер этого сопротивления иной, чем при прямолинейном движении, поскольку гусеницы, продолжая перекатываться, кроме того, поворачиваются. Чтобы ясно представить себе, что происходит в этом случае, рассмотрим поворот отдельной гусеницы (рис. 478).
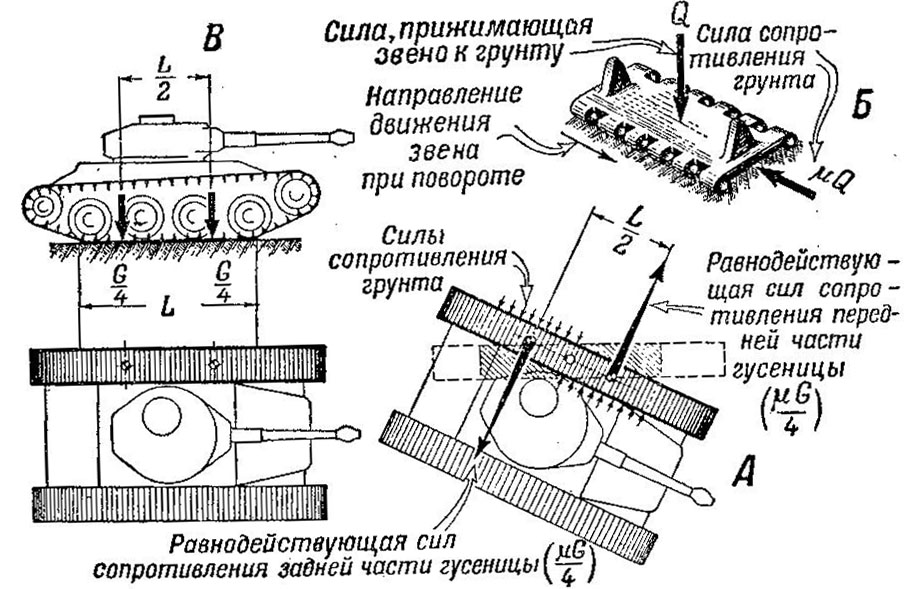
Рис. 478. Сопротивление повороту отдельной гусеницы при равномерном распределении веса танка по длине опорной поверхности
Пусть опорная ветвь гусеницы поворачивается вокруг своего центра (положение А). Передняя половина опорной ветви гусеницы движется вправо, задняя — влево, причем звенья смещаются вбок. При повороте сила трения звеньев о грунт и противодействие грунта разрушению будут создавать сопротивление повороту. Величина его зависит от силы, прижимающей траки к грунту, характера самого грунта и устройства гусеницы.
Силу сопротивления повороту можно определить, если знать коэффициент сопротивления повороту μ.Определяемый опытным путем, этот коэффициент показывает, какая связь существует между силой, прижимающей звенья к грунту, и сопротивлением при повороте, подобно тому как коэффициент f показывает эту связь при прямолинейном движении. Если звено прижато к грунту силой Q, сила сопротивления будет равна μQ(рис. 478,Б).
Силы сопротивления действуют на каждое звено опорной ветви гусеницы. Эта силы можно заменить их равнодействующей. Из рис. 478, А видно, что равнодействующие сил сопротивления, действуя на переднюю и заднюю половины гусениц, создают пару сил, препятствующую повороту гусеницы танка.
Если считать, что вес танка распределяется поровну между обеими гусеницами и равномерно по их длине, то на каждую из гусениц придется половина веса танка G/2, а на половину гусеницы - четверть веса G/4 (рис. 478, В).Величина каждой равнодействующей составляет поэтому μG/4 (рис. 478, А).
Плечо пары сил равно половине длины опорной поверхности гусеницы, т. е. L/2
Следовательно, момент пары равен
μG / 4 x L / 2 = μGL / 8
Такой же момент действует на вторую гусеницу. Общий момент сопротивления повороту будет
2μGL / 8 = μGL / 4
В действительности величина и распределение сил, действующих на гусеницы ири повороте, будут иными, чем это показано на рис. 478. В предыдущих рассуждениях предполагалось, что опорная ветвь гусеницы поворачивается вокруг своего центра. На самом деле. это не совсем так. Как уже говорилось, опорные ветви проскальзывают по грунту (буксование и юз) и поэтому не только поворачиваются, но и смещаются вперед или назад. Следовательно, опорная ветвь поворачивается вокруг точки, не совпадающей с ее центром. Эта точка называется полюсом поворота опорной ветви (рис. 479).
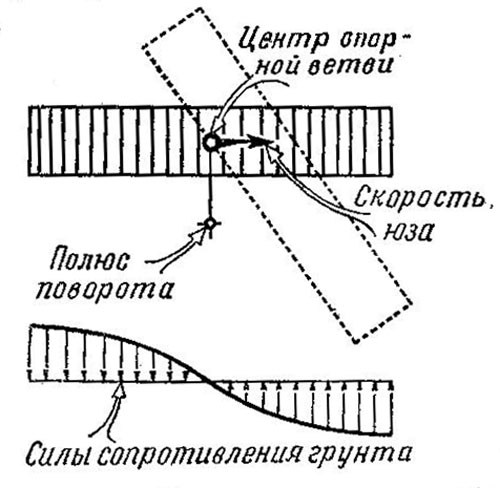
Рис. 479. Полюс поворота опорной ветви при продольном скольжении не совпадает с центром ветви
Силы же сопротивления грунта будут уменьшаться от краев опорной ветви к полюсу, как показано на том же рисунке. Чтобы не усложнять исследование явления поворота, в дальнейшем мы не будем принимать эти обстоятельства во внимание, т. е. будем считать, что полюс поворота опорной ветви лежит в ее центре.
СИЛА ТЯГИ И ТОРМОЗНАЯ СИЛА
Чтобы танк повернулся, момент пары РВ (см. рис. 477), поворачивающей танк, должен быть больше момента сопротивления, или, по крайней мере, равен ему, т. е.
РВ = μGL / 4
откуда
Р = μGL / 4В
Такую величину должны были бы иметь сила тяги на забегающей гусенице и тормозная — на отстающей, если бы гусеницы преодолевали только боковое сопротивление; но при повороте танка каждая гусеница, перекатываясь, преодолевает сопротивление качению
R= fG / 2 ,
где f—-коэффициент сопротивления качению
G/2— вес, приходящийся на одну гусеницу.
Сопротивление качению на забегающей гусенице направлено против силы тяги, т. е. препятствует повороту. Значит, силу тяги Р2на забегающей гусенице надо увеличить на величину fG/2
или
Р2= μGL / 4В + fG / 2
На отстающей гусенице сила сопротивления качению Rнаправлена в ту же сторону, что и тормозная сила. Она помогает тормозной силе тормозить гусеницу; поэтому тормозная сила Р1на отстающей гусеницедолжна быть уменьшена на ту жевеличину, т. е.
Р1= μGL / 4В — fG / 2
Схема сил, действующих на гусеницы при повороте, показана на рис. 480.

Рис. 480. Силы, действующие на танк при повороте
Здесь вместо сил сопротивления повороту даны их равнодействующие.
Сила тяги на забегающей гусенице создается двигателем. Чтобы танк повернулся, двигатель должен обеспечить эту силу. Как видно из формулы, сила тяги Р2 при повороте зависит от веса танка G, длины опорной поверхности L, ширины колеи В и коэффициентов сопротивления μи f.
Как и при прямолинейном движении, сила тяги должна быть тем больше, чем тяжелее танк. Но, в отличие от прямолинейного движения на величину силы тяти при повороте существенно влияют размеры танка, поскольку длина опорной поверхности Lзависит от длины танка, а ширина колеи В — от ширины танка.
Чем короче опорная поверхность Lи шире колея В, тем меньшая сила тяги требуется от двигателя для поворота, тем легче будет поворачиваться танк.
Для танков отношение L/Bнаходится в (пределах 1,1—1,8. При очень
больших значениях L/B например 2,5—3, танк вряде случаев вообще
не сможет поворачиваться, так как сцепление гусениц с грунтам может оказаться недостаточным, и забегающая гусеница забуксует. Действительно, сила тяги по сцеплению Рс для одной гусеницы равна коэффициенту сцепления φ, умноженному на половину веса G/2или (приφ= 0,8) Pс=0,4G; при большом отношении L/B нужная для поворота сила тяги Р2 может оказаться больше силы тяти по сцеплению.
КОЭФФИЦИЕНТ СОПРОТИВЛЕНИЯ ПОВОРОТУ И РАДИУС ПОВОРОТА
Коэффициент сопротивления повороту μзависит не только от качества грунта и устройства гусеницы, как коэффициенты fи φно и от радиуса поворота танка.
При повороте танка погружающиеся в грунт гусеницы разрушают его своимикромками и шпорами эвеньев, а при кругых поворотах на мягком грунте нагребают земляной вал из срезанного грунта. Чем круче поворот, тем сильнее разрушается грунт и тем больше препятствует повороту танка земляной вал. 3начит, при малых радиусах поворота сила сопротивления уведачивается, а следовательно, увеличивается и коэффициент μ.При больших радиусах поворота, наоборот, сопротивление уменьшается.
На равных грунтах величина коэффициента μ и характер ее изменения в зависимости от радиуса поворота различны. На твердом грунте на звенья гусениц действуют главным образом силы трения, поэтому коэффициент будет меньше, чем на мягком грунте, на котором большое значение имеет срез и нагребание земли. С увеличешем радиуса поворота на твердом грунте коэффициент изменяется незначительно. На мягком грунте крутой поворот приведет к значительному увеличению коэффициента сопротивления. Примерный характер изменения коэффициента на мягком грунте показан на графике (рис. 481).
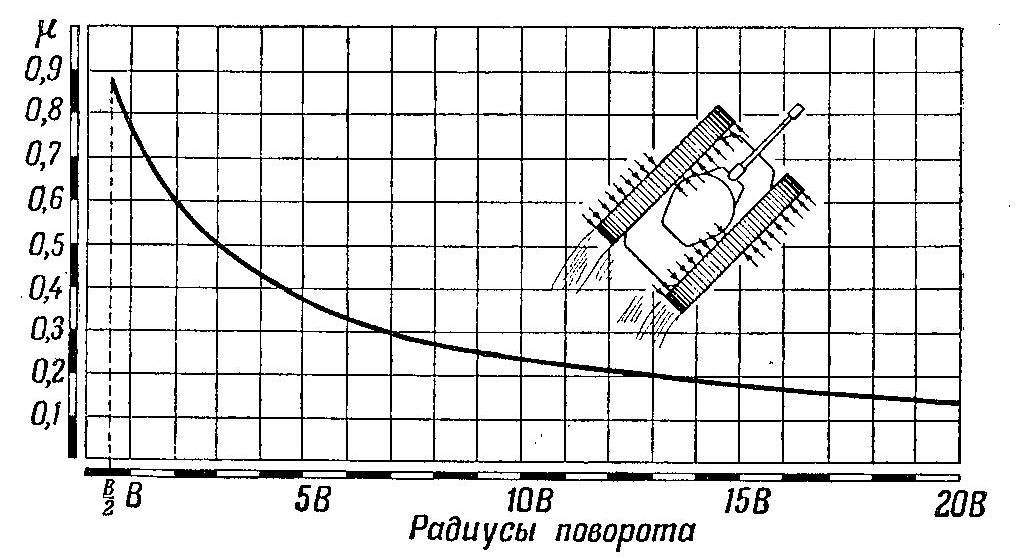
Рис. 481. Изменение коэффициента μв зависимости от изменения радиуса поворотатанка на мягком грунте
На основании этого графика подсчитаны силы Р2 и Р1 изменение которых в зависимости от радиуса поворота (конечно, для данного грунта) показано на графике (рис. 482).
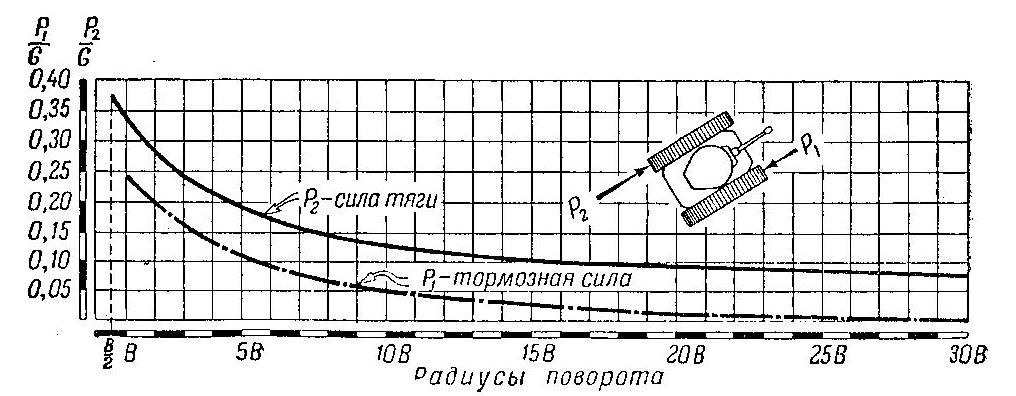
Рис. 482. Изменение силы тяги итормозной силы в зависимости от радиусаповорота танка
Графиком можно пользоваться для танка любого веса, так как на нем приведены не сами величины сил, а их отношениек весу танка, т. е, Р2 и Р1 (удельные силы), причем для прямолинейного движения удельная сила тяги P/G принята равной 0,08, а L/B= 1,6.
Зная вес танка, можно по удельным силам определить и самисилы Р2 и Р1.Так, для радиуса поворота R= 5B находим по графику Р2 / G = 0,19 и Р1 / G = 0,11. Если вес танка G = 30 т, соответствующиесилы будут равны: cила тяги Р2 = 0,19 • 30 = 5,7 т, тормозная сила Р = 0,11 • 30 =3,3 т.
Как видно из графика, сила тяги Р2 с увеличением радиуса поворота уменьшается сначала быстро, затем все медленнее. Это объясняется характером уменьшения коэффициента сопротивления повороту. Отметим, что сила тяги при повороте имеет большую величину, чем при прямолинейном движении на том же грунте, и лишь при весьма большом радиусе поворота (R= 30B, т. е. 60—90 м) приближается к ней. При большом радиусе поворота взаимодействие гусениц с грунтом мало отличается от взаимодействия при прямолинейном движении. Действительно, для такого поворота достаточно, чтобы гусеница изогнулась за счет зазоров вшарнирах, соединяющих звенья, как это схематически показано на рис. 483.

Рис. 483. Танк может поворачиваться за счет изгиба гусениц
Величина необходимых для этого зазоров в шарнирных соединениях соседних звеньев составляет десятые доли миллиметра.
Тормозная сила Р1 также уменьшается с увеличением радиуса. При радиусе около 30В она становится равной нулю. Практически это означает, что на радиусе поворота 30 В и больше танк поворачивается без торможении отстающей гусеницы. Пара сил, нужная для поворота, создается силой тяги на забегающей гусенице и силой сопротивления качению на отстающей. Для поворота достаточно отключить отстающую гусеницу от двигателя, не притормаживая ее.
Поворот с радиусом больше 30 В, т. е. 60—90 м и более, необходим для того, чтобы заставить танк «следить» за кривизной дорога, или для выравнивания танка при отклонении (уводе) его в сторону от принятого курса; в дальнейшем будет рассматриваться лишь поворот, при котором на отстающей гусенице создается тормозная сила, т. е. поворот с радиусом не более 30 В.
ЗАНОС ТАНКА И ПРЕДЕЛЬНАЯ СКОРОСТЬ ПРИ ПОВОРОТЕ
Как и на всякое (вращающееся тело, на танк при повороте действует центробежная сила инерции, приложенная к центру тяжести танка. Эта сила стремится «занести» танк в сторону. Вместе с тем грунт, действуя на гусеницы, препятствует заносу (рис. 484).
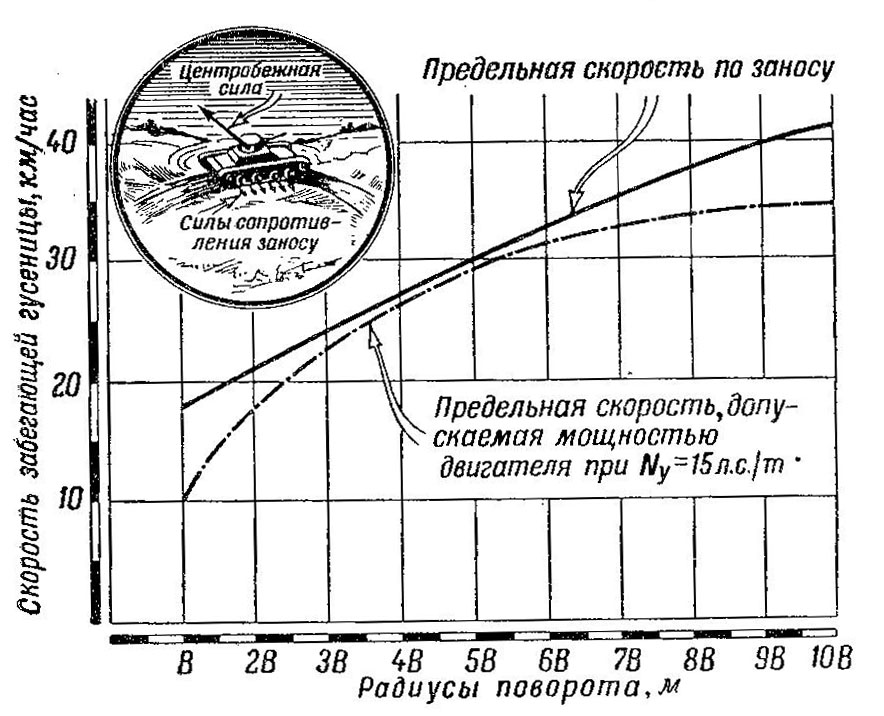 Рис. 484. Занос танка при повороте
Рис. 484. Занос танка при повороте
Занос станет возможным, если центробежная сила превысит силу сопротивления грунта.
Величина центробежной силы С, действующей на тело, определяется формулой механики
C = Mv2 / R0
где М—масса тела;
v— скорость его центра тяжести;
R0= R– B/2 - радиус вращения.
Из формулы следует, что центробежная сила увеличивается с увеличением скорости танка и уменьшением радиуса поворота. Так как с увеличением веса танка возрастает сила сопротивления грунта, то вес танка не влияет на занос.
Верхняя кривая на рис. 484 .показывает предельную скорость забегающей гусеницы, при которой на данном радиусе еще возможен поворот танка без заноса. Эта скорость определена для местности с достаточно твердым грунтом (μ= 0,6), причем значение μв данном случае не зависит от радиуса поворота, так как гусеницы в любом случае перемещаются в поперечном направлении. На скользком грунте, размытом дождем, и особенно на льду сопротивление невелико, ввиду чего опасность заноса значительно увеличивается и допустимая скорость падает.
Нижняя кривая на том же рисунке показывает, какую скорость в действительности может иметь забегающая гусеница при удельной мощности двигателя 15 л. с./т. На некоторых радиусах нижняя кривая приближается к верхней; в этих случаях возможность заноса увеличивается. Иногда механизмы поворота автоматически ограничивают возможность поворота на малых радиусах или не позволяют поворачиваться на этих радиусах при больших скоростях движения. При поворотах на малых радиусах с небольшими скоростями занос почти невозможен даже на скользких грунтах.
Заметим, что центробежная сила и сила сопротивления заносу (рис. 484, в круге) образуют пару сил, плечо которой равно высоте центра тяжести. Эта пара стремится опрокинуть танк. Вероятность опрокидывания обычно возникает при большей скорости, чем возможность заноса, т. е. танк заносит раньше, чем начинается опрокидывание. Лишь в том случае, когда под гусеницей окажется препятствие, увеличивающее сопротивление поворогу (кочка, бугор), опрокидывание может произойти раньше заноса.
Возможность опрокидывания наиболее вероятна для танков с высоко расположенным центром тяжести, так как в этом случае увеличивается плечо и момент пары сил, опрокидывающей танк. Современные советские танки при повороте вообще не могут опрокинуться.
МОЩНОСТЬ ПРИ ПОВОРОТЕ
Сопротивление грунта при повороте танка значительно выше, чем при прямолинейном движении, поэтому для поворота при равных средних скоростях требуется большая мощность, чем для прямолинейного движения. Если двигатель не в состоянии обеспечить нужную мощность, необходимую силу тяги придется получить путем снижения скорости танка. Когда танк движется прямолинейно, в его механизмах теряется обычно около 30% мощности двигателя, при повороте эти (потери могут составить 60—70%, а иногда и больше. В этом случае величина потерь зависит от того, каким способом достигается изменение скорости отстающей гусеницы и создание тормозной силы, т. е. от устройства механизмов поворота.
На танках устанавливались механизмы поворота самых различных типов: бортовые фрикционы, одноступенчатые и многоступенчатые пла-нетарные механизмы, простые и двойные дифференциалы и др. Все эти механизмы устроены по-разному, и на первый взгляд между ними мало общего. Однако все они имеют одно и то же назначение. Их работу можно уяснить на примере наиболее лростых механизмов двух-трех типов. Такими простыми механизмами являются, например, бортовые коробки передач.
Бортовые коробки передач устанавливались в свое время на некоторых танках, но давно уже не применяются. Тем не менее на примере бортовых коробок удобнее всего проследить, какие явления происходят при повороте, и выяснить, чем определяется необходимая для поворота мощность. Выводы, сделанные при этом, могут быть полностью отнесены к большинству современных механизмов поворота, а в той или иной степени — и ко всем механизмам.
ПОВОРОТ НА РАСЧЕТНЫХ РАДИУСАХ
Пусть на каждом борту танка установлена обычная коробка передач, как показано на рис. 485.
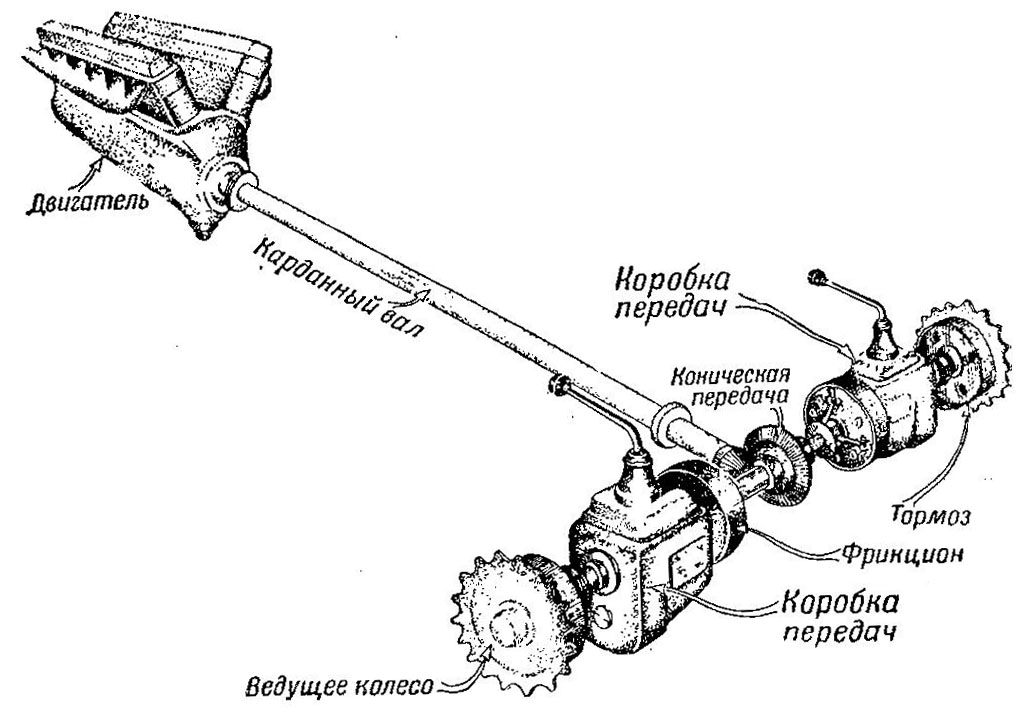
Рис. 485. Бортовые коробки передач могут служить механизмами поворота танка
Обе коробки устроены одинаково. Ведущий вал каждой из них через коническую передачу и карданный вал связан с коленчатым валом двигателя, ведомый вал соединен с одним из ведущих колес танка.
Рассмотрим работу этих коробок.
ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
Включим в обеих коробках одинаковые передачи. Ведущие колеса в этом случае будут иметь равное число оборотов, и танк будет двигаться прямолинейно. Мощность двигателя подводится к обеим гусеницам и затрачивается на преодоление сопротивления прямолинейному движению.
На горизонтальном участке пути при коэффициенте сопротивления качению f= 0,08 сила тяги обеих гусениц будет равна Р = 0,08G,
В предыдущей главе было показано, что между силой тяги и мощностью двигателя существует связь, определяемая формулой
NД = 5Pv
Подставив значение Pполучим
NД= 5 x 0,08Gv = 0,4Gv
Заметим, что в данном случае это не наибольшая мощность двигателя, которую он может развивать, а мощность, необходимая для преодоления сопротивления движению танка, называемая мощностью внешних сопротивлений и обозначаемая N0. Тогда
N0 = 0.4Gv
ПОВОРОТ ВОКРУГ ЦЕНТРАЛЬНОЙ ОСИ ТАНКА
Включим в одной из коробок первую передачу, а в другой задний ход. Пусть скорость заднего хода равна скорости первой передачи. Тогда гусеницы получат равные по величине скорости, направленные в разные стороны, и танк будет поворачиваться вокруг своей центральной оси.
Заметим, что в этом случае сила Р1на отстающей гусенице является не тормозной силой в обычном понимании, а такой же силой тяги, как и сила Р2на забегающей гусенице. Она создается двигателем. Направление ее противоположно направлению силы на забегающей гусенице. Отсюда легко сделать заключение, что обе силы тяги равны, а раз равны и скорости гусениц, то одинаковы, и мощности, подводимые к ним от двигателя.
Считая, что поворот происходит на грунте, для которого составлен график (рис. 482), возьмем из графика значение силы Р2для R = B/2; получим мощность для забегающей гусеницы
N2 = 5 P2v2 = 5 x 0,38Gv2 = 1,9 Gv2
а для обеих гусениц
2N2= N0= 3,8Gv2
Мощность внешних сопротивлений будет в этом случае
N0= 3,8Gv2
где v2 — скорость забегающей гусеницы.
При равных скоростях эта мощность почти в 10 раз больше мощности, требующейся для прямолинейного движения.
ПОВОРОТ ВОКРУГ ОДНОЙ ИЗ ГУСЕНИЦ (R=B)
Включим в одной из коробок какую-нибудь передачу, например первую, а другую коробку оставим в нейтральном положении, т. е. отклю-чим вторую гусеницу от двигателя. К отключенной гусенице крутящий момент от двигателя подводиться не будет.
В этом случае танк будет двигаться почти прямолинейно, так как отстающая гусеница, связанная корпусом танка с забегающей гусеницей, будет перемещаться вперед. Для поворота надо создать на отстающей гусенице тормозную силу. Затянем тормоз полностью, т. е. так, чтобы гусеница остановилась. Танк будет поворачиваться вокруг заторможенной гусеницы с радиусом поворота R= В(проскальзыванием пренебрегаем),
В отличие от поворота вокруг центральной оси танка, в данном случае мощность двигателя подводится только к забегающей гусенице, так как отстающая отключена.
Взяв из графика (см. рис. 482) силу Р2 для R = B получим
N0= 5 х 0,34Gv2
или
N0= 1,7Gv2
Мощность внешних сопротивлений будет в 2 с лишним раза меньше, чем в предыдущем случае. Уменьшение мощности достигнуто путем увеличения радиуса поворота.
ПОВОРОТ С РАДИУСОМ, БОЛЬШИМ ШИРИНЫ КОЛЕИ (К>В)
Теперь включим в одной из коробок вторую передачу, а в другой первую. Скорость одной из гусениц (забегающей) будет больше, чемскорость другой (отстающей).
Как и в том случае, когда отстающая гусеница отключена, забегающая гусеница через корпус танка стремится увлечь ее с той же скоростью, с какой движется она сама. Но ведущее колесо отстающей гусеницы может иметь только строго определенное число оборотов, соответствующее передаточному числу первой передачи. Следовательно, гусеница не только не сможет быстрее провернуть ведущее колесо, но и сама будет тормозиться им.
Разница по сравнению с поворотом вокруг полностью заторможенной отстающей гусеницы будет лишь в том, что тормоз удерживает ведущее колесо неподвижно, а включенная передача коробки позволяет ему вращаться с определенной скоростью. Эта скорость будет меньше той, которую стремится сообщить ведущему колесу гусеница. На отстающей гусенице, притормаживаемой ведущим колесом, возникает тормозная сила. Сила тяги на забегающей гусенице и тормозная сила создают пару сил, которая и будет поворачивать танк.
Как мы уже говорили, радиус поворота в этом случае больше ширины колеи. Величина этого радиуса вполне определенная: она зависит от передаточных чисел коробок, т. е. от отношения скоростей обеих гусениц.
Допустим, например, что передаточное число второй передачи i2= 5, а первой i1= 10. Если число оборотов двигателя nд = 2000 в минуту, ведущее колесо забегающей гусеницы будет делать n2 = 2000/5 = 400 об/мин а отстающей n1=2000/10 = 200 об/мин,т.е. вдвое меньше.
Скорость забегающей гусеницы будет поэтому вдвое выше скорости отстающей.
Если изобразить скорости забегающей и отстающей гусениц в виде стрелок (рис. 486) и соединить концы стрелок прямой линией, получим два подобных прямоугольных треугольника, вершины которых лежат в центре поворота (где скорость равна нулю), катет одного равен радиусу поворота R, а другого R— В.
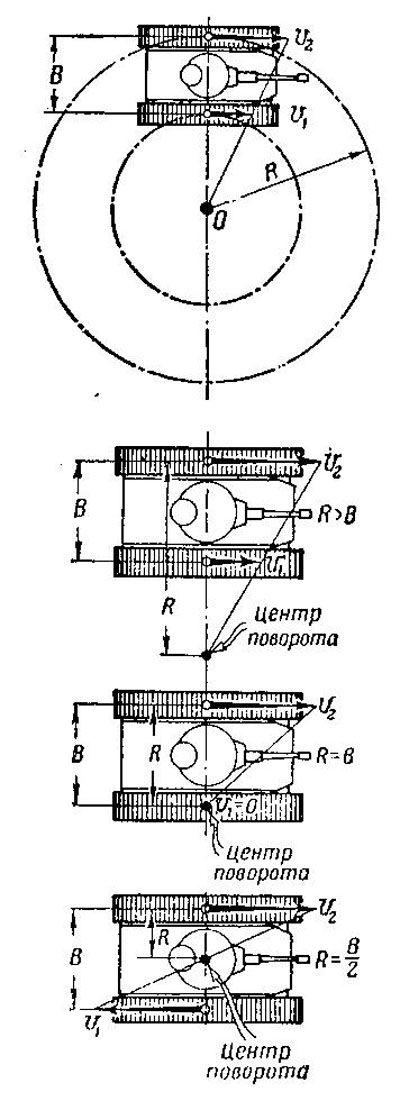
Рис. 486. Графический способ определения радиуса поворота танка
Из подобия треугольников следует, что
v1/ v2= (R – B)/R = 1 – B/R (10)
На рис. 486, кроме поворота с радиусом R > В , показаны также повороты танка с радиусами R = В и R = B/2.
В нашем примере v1/v2=1/2 тогда из приведенного соотношения (10) можно определить радиус поворота R
R= 2B
Перейдем теперь к определению мощности внешних сопротивлений при радиусе поворота больше В.
циркуляция мощности
Особенность передачи мощности при повороте в этом случае заключается в том, что здесь происходит циркуляция мощности, т. е, передача мощности от отстающей гусеницы к забегающей. Чтобы уяснить это явление, рассмотрим следующий пример.
Представим себе, что гусеницы танка сняты, оба ведущих колеса напрямую соединены с двигателем (рис. 487) и к ним приложены равные сопротивления (например, частично затянуты тормоза, не показанные на рис. 487).

Рис. 487. Пример к вопросу о циркуляции мощности
Колеса вращаются с одинаковой скоростью. Пусть от двигателя к каждому колесу подводится одинаковая мощность, скажем 50 л. с., а всего двигатель развивает мощность 100 л. с, которая расходуется на преодоление сопротивлений, приложенных к ведущим колесам.
При помощи показанного на рис. 487 тормоза частично притормозим одно из-ведущих колес, поддерживая при этом обороты двигателя постоянными. Для этого надо увеличить подачу горючего. Число оборотов обоих колес останется прежним. Но к приторможенному колесу теперь будет подводиться большая мощность. Если дополнительная мощность, расходуемая в тормозе, равна 50 л. с, двигатель должен будет давать уже 150 л.с., из которых 50 л. с. пойдет к левому колесу, а 100 л. с.— к правому (рис 487,Б):
Если теперь, отпустив тормоз, соединить правое ведущее колесо с посторонним источником энергии (скажем, с электромотором), который будет вращать ведущее колесо, двигателю уже не придется затрачивать дополнительную мощность (рис. 487,В). Больше того, если мощность электромотора больше, чем требуется для вращения одного колеса, например 75 л. с., то он не только будет вращать его, но а поможет двигателю вращать второе колесо. В нашем примере из 75 л. с, общей мощности электромотора 50 л. с. будут тратиться на вращение правого колеса, а остальные 25 л. с. передадутся левому. От основного двигателя теперь потребуется всего лишь 25 л, с, причем вся эта мощность пойдет к левому колесу, а к правому колесу мощность двигателя вообще не будет подводиться. Следовательно, чтобы поддержать прежние обороты, нужно будет уменьшить подачу горючего.
Теперь допустим, что гусеницы надеты и танк движется. С правым ведущим колесам танка связан якорь генератора, а с левым — якорь электромотора (рис. 488).
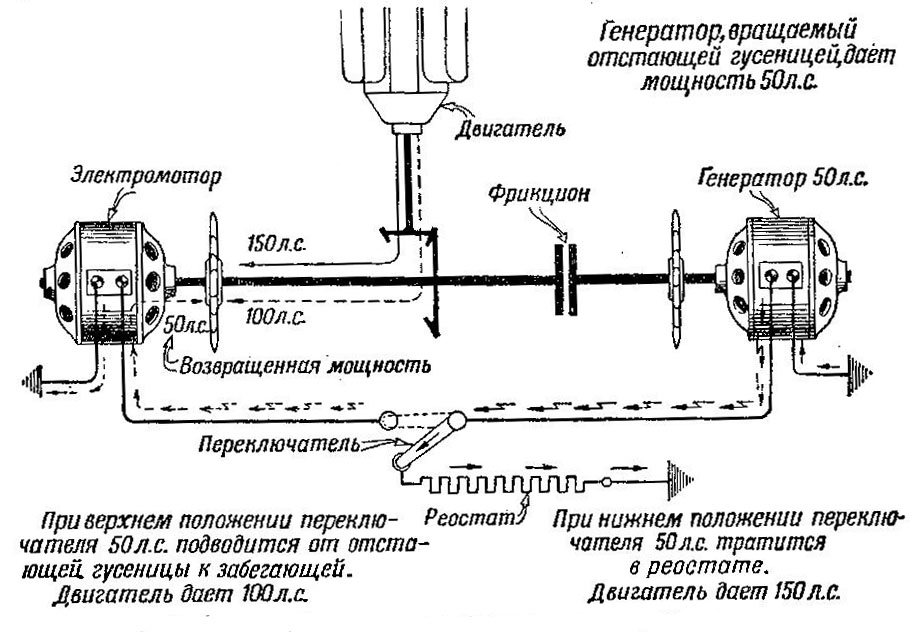
Рис. 488. Циркуляция мощности в электрической схеме
Генератор и электромотор соединены между собой проводами через переключатель. Отключим правое ведущее колесо от двигателя, например при помощи фрикциона. Забегающая левая гусеница через корпус танка стремится сообщить отстающей ту же скорость, с какой вращается она сама. Но якорь генератора через правое ведущее колесо притормаживает отстающую гусеницу. На ней создается тормозная сила, направленная назад. Под действием пары сил — силы тяги и тормозной силы — танк будет поворачиваться.
На вращение якоря генератора затрачивается мощность. Откуда же и как она поступает к отстающей гусенице, которая отключена от двигателя? Точно так же, как подводится мощность к передним колесам автомобиля, у которого только задние колеса являются ведущими. Задние ведущие колеса толкают вперед корпус (раму) автомобиля вместе с передними колесами.
Сила оцепления передних колес с грунтом заставляет их вращаться, преодолевая сопротивление качению..
Грунт, на который опирается танк, играет в этом случае роль приводного ремня, передающего мощность от одного шкива к другому. Часть мощности, переданной от двигателя на задние колеса, через грунт идет к передним. Точно так же часть мощности, переданной двигателем на забегающую гусеницу, переходит при посредстве грунта, на который опирается танк, на отстающую гусеницу. За счет этой мощности и вращается якорь генератора.
Пусть от двигателя к забегающей гусенице поступает мощность 150 л. с, из них 100 л. с. тратится на преодоление сопротивления грунта и 50 л. с. передается генератору. Ток, выработанный генератором, идет креостату и нагревает его; в реостате мощность тратится бесполезно.
Повернув переключатель (рис. 488) в верхнее положение, замкнем цепь тока генератор (на отстающей гусенице) — мотор (на забегающей). Тогда ток, вместо того чтобы идти в реостат, пойдет к электромотору. Электромотор начнет работать, помогая двигателю, как и в предыдущем примере (см. рис. 487, В), вращать ведущее колесо забегающей гусеницы. Разница лишь в том, что в предыдущем примере электромотор питался током от постороннего источника, а в данном случае он питается от генератора, поставленного на самом танке.
Мощность генератора, попрежнему равная 50 л. с, теперь передается электромотору. Но к забегающей гусенице требуется подводить мощность 150 л. с. Значит, двигатель должен давать 150 — 50= 100 л. с. вместо 150 л. с. Отстающая гусеница возвращает забегающей полученную ею мощность (за вычетом части мощности, затраченной на преодоление сопротивления грунта). Таким образом, сберегается 50 л. с. мощности двигателя.
Вернемся теперь к танку с бортовыми коробками передач.
Отстающая гусеница, как мы видели, толкает ведущее колесо вперед, стремясь вращать его быстрее, чем это возможно при включенной первой передаче. Хотя передача и включена, мощность от двигателя к этому ведущему колесу не подводится. Наоборот, гусеница, толкая ведущее колесо, сама передает ему мощность, как она передавала ее генератору в только что рассмотренном примере.
Через валы и шестерни коробок мощность возвращается на забегающую гусеницу. От двигателя поэтому требуется меньшая мощность.
Все время, пока танк поворачивается, часть мощности циркулирует между забегающей и отстающей гусеницами по кругу забегающая гусеница — грунт — отстающая гусеница — правая коробка передач — левая коробка передач — забегающая гусеница. Это циркулирующая (холостая) мощность; она не производит никакой работы. Если бы она совершала работу (хотя бы нагревала реостат, как в нашем примере), она не возвращалась бы к забегающей гусенице и не приводила бы к уменьшению мощности, которую должен дать двигатель.
Циркулирующая мощность возникает в тот момент, когда танк начинает поворачиваться. Рассмотрим, как это происходит.
Предположим, что вначале правую гусеницу отключили (см. рис. 485). Тогда правая часть вала, соединяющего коническую передачу с коробками передач, не несет никакой нагрузки, поскольку вся мощность двигателя идет к левой коробке. Допустим, что передача в коробке отстающей гусеницы включается плавно (позже мы убедимся, что это так и происходит благодаря фрикциону). Включим в ней первую передачу. Как только начнется включение, отстающая гусеница будет стремиться ускорить вращение вала конической передачи. Но это невозможно, так как обороты вала определяются оборотами двигателя.
Поэтому ведущее колесо отстающей гусеницы будет закручивать правую часть вала конической передачи, само удерживаясь (тормозясь) моментом той же величины, с которой она закручивает вал; этот момент и создаст тормозную силу Р. Но вал закручивается в направлении своего вращения. Следовательно, закручивающий его момент будет добавляться к крутящему моменту двигателя, облегчая его работу, В этом и заключается сущность явления циркуляции мощности.
Когда поворот танка с радиусом R> Bпроисходит при циркуляции мощности, мощность двигателя, как и в рассмотренных нами ранее случаях, тратится только на преодоление внешних сопротивлений.
Радиус поворота, при котором вся мощность тратится только на преодоление внешних сопротивлений, называется расчетным и обозначается Rр.
Величина расчетных радиусов при бортовых коробках вполне определенная: она зависит от того, какие передачи включены. Поворот на расчетном радиусе устойчив.
ПОТРЕБНАЯ НА ПОВОРОТ МОЩНОСТЬ
Такям образом, если Rрбольше В, к забегающей гусенице подводится мощность N2из двух источников: от двигателя поступает мощность Nо, которая тратится на преодоление внешних сопротивлений, и от отстающей гусеницы — возвращаемая (циркулирующая) мощность N1 так что N2 = N0 + N1
Величина мощности, подводимой к забегающей гусенице, определяется силой тяги и скоростью и может быть, как и во всех других случаях, найдена по формуле 5P2v2. Oчевидно, то же относится к отстающей гусенице; на ведущее колесо со стороны этой гусеницы действует тормозная сила P1при скорости v1. Таким образом, можно написать
5P2v2 = N0 + 5P1v1
Отсюда можно определить мощность, которую должен дать двигатель и которая пойдет на преодоление сил сопротивления повороту, т. е. мощность внешних сопротивлений
N0 = 5(P2v2 - P1v1 ) (11)
Но, как мы видели выше в формуле (10) для случая R > B,
v1 / v2 = 1 - B/R
Подставляя значение v1 / v2в формулу (11), получим окончательно
N0 = 5(P2 - P1 (1- B/R))v2 (12)
Определим N0 для R= 2В. Из графика (см. рис. 482) находим P2 = 0,28Gи P1= 0,2G. Тогда

Таким образом:
— при Rp = B/2 (первая передача и задний ход) N0= 3,8 Gv2;
— при Rр = В (первая передача и заторможенная отстающая гусеница) N0= 1,7 Gv2;
— при Rр=2B (вторая передача и первая передача) N0= 0.9 Gv2;
Чем больше расчетный радиус, тем меньшая удельная мощность необходима для поворота. То же следует и из выведенной нами формулы (12).
На рис. 489 приведен график зависимости мощности внешних сопротивлений от расчетного радиуса, построенный по формуле (12).

Рис.489 Удельная мощность внешних сопротивлений в зависимости от радиуса поворота при скорости забегающей гусеницы v2= 1 км/час
Дляудобства пользования графиком даны удельные мощности, т. е. N0 / G,
а скорость забегающей гусеницы принята равной 1 км/час. Чтобы определить мощность при повороте танка, например, весом 30 т при v2=10 км/час с радиусом Rр= 10 В, берем из графика величину N0у= 0,43 и, умножая на вес и скорость, находим N0= 0,43х30х10 = = 129 л. с.
Из графика следует, что мощность внешних сопротивлений умень--шается по мере увеличения радиуса поворота. Это объясняется тем, что мощность внешних сопротивлений при повороте определяется моментом, создаваемым силами сопротивления повороту, и угловой скоростью поворота, С увеличением радиуса поворота уменьшается и момент сопротив-ления (из-за снижения коэффициента μ) и угловая скорость.
Выше рассматривался пример, когда были включены первая и вторая передачи бортовых коробок. Можно включить первую и третью или первую и четвертую передачи. В этих случаях увеличится отношение между скоростями забегающей и отстающей гусениц и уменьшится радиус поворота, а потому возрастет мощность внешних сопротивлений. Вместо первой и второй передач можно включить третью и четвертую, при этом расчетный радиус (поворота изменится незначительно, но зато возрастет угловая скорость поворота, так как увеличится скорость забегающей гусеницы.
Число расчетных радиусов зависит от числа передач коробок. Применяемые на танках механизмы обычно соответствуют коробкам передач не более чем с двумя передачами, что дает два расчетных радиуса поворота (вторая — первая передача и одна из передач с нейтралью и тормозом).
ПОВОРОТ НА РАДИУСАХ, ОТЛИЧАЮЩИХСЯ ОТ РАСЧЕТНОГО
ПРОМЕЖУТОЧНЫЕ РАДИУСЫ ПОВОРОТА
Рассмотренные нами бортовые коробки обеспечивают определенное число расчетных радиусов. Это число увеличивается при увеличении количества передач коробок, Применение непрерывных коробок передач дало бы возможность поворачиваться с любым расчетным радиусом.
Так как ступенчатые коробки ограничивают количество расчетных радиусов поворота, то среди них может не оказаться того радиуса, который необходим по условиям движения.
Чтобы танк имел возможность поворачиваться с любыми, а не только с расчетными радиусами, поставим в дополнение к коробкам передач по фрикциону (рис. 490).

Рис. 490 Потребная мощность при повороте без пробуксовкии с пробуксовкой фрикциона
Включим на забегающей гусенице вторую, а на отстающей — первую передачу. Допустим, что расчетный радиус будет при этом Rр==2B. Если по условиям движения необходимо поворачиваться с радиусом больше 2В, например с R= 10В, то для этого при неизменной скорости забегающей гусеницы нужно увеличить ско рость отстающей,
Заставим фрикцион отстающей гусеницы слегка пробуксовывать. Для этого, уменьшив нажатие на диски, дадим возможность ведущей и ведомой частям фрикциона вращаться с разными скоростями, но так, чтобы фрикцион не был полностъю выключен. Теперь отстающая гусеница, увлекаемая забегающей, сможет вращаться с большей скоростью, чем это позволяет передаточное число первой передачи. Так, если без пробуксовки при включенной первой передаче ведущее колесо делает 200 об/мин и нельзя изменить его обороты, не меняя числа оборотов дви гателя, то пря пробуксовке фринциона колесо может делать и 250, и 300, и любое большее числооборотов, но, конечно, не больше, чем делает ведущее колесо забегающей гусеницы: отстающую гусеницу ведет забегающая, обогнать которую отстающая гусеница не может.
Чем больше пробуксовка фрикциона, там меньше разница между скоростью отстающей гусеницы и скоростью забегающей и тем больше радиус поворота танка. Когда фрикцион выключится полнюстью, скорости обеих гусениц почти сравняются, и танк будет двигаться почти прямолинейно, с небольшим уводом в сторону отстающей гусеницы (как это бывает всегда, когда на отстающей гусенице не создается тормозная сила).
При помощи дополнительного фрикциона танк может поворачиваться с любым радиусом, лишь бы он был больше расчетного (в нашем примере больше 2В). По мере уменьшения пробуксовки скорость отстающей гусеницы уменьшается до тех пор, пока действительный радиус поворота Rне станет равен расчетному, т. е, равному 2В. Чтобы еще уменьшить радиус поворота, надо еще больше снизить скорость отстающей гусеницы. На данной передаче этого сделать нельзя. Надо переходить к низшему расчетному радиусу.
Благодаря пробуксовке фрекциона можно как угодно увеличивать радиус поворота сверх расчетного, но не уменьшать его. Расчетный радиус, следовательно, является наименьшим для данной передачи.
Поворот с буксованием фрикциона неустойчивый, так как в данном случае скорость отстающей гусеницы не бывает определенной. Она изменяется в зависимости от сопротивлений, которые преодолевает танк; при этом изменяется и радиус поворота.
ПОТЕРЯ МОЩНОСТИ
Таким образом, даже при наличии единственного расчетного радиуса танк может совершать поворот с любым радиусом, лишь бы он был больше расчетного. Однако такой поворот сопровождается буксованием фрикциона, а следовательно, потерей мощности на трение. Чтобы выяснить величину потерь в фрикционе, вернемся к повороту танка на расчетном радиусе.
Пусть ведущий вал фрикциона делает 2000 об/мин (рис. 490, вверху). Фрикционы не буксуют, и их ведомые валы также делают по 2000 об/мин. При включенных передачах коробок левое ведущее колесо делает 400 об/мин, правое 200 об/мин. Соответственно скорость левой гусеницы будет вдвое больше правой, например 20 и 10 км/час. Отстающая (правая) гусеница, стремясь развить скорость 20 км/час, толкает свое ведущее колесо вперед. Через коробку и фрикцион передается на забегающую гусеницу мощность, равная, скажем, 50 л, с. Эта мощность определяется тормозной силой и скоростью отстающей гусеницы. Двигатель развивает мощность 100 л. с, равную мощности внешних сопротивлений, а всего на забегающую гусеницу поступает 150 л. с.
Теперь дадим правому фрикциону возможность пробуксовывать (рис. 490, внизу). Частично освобожденное ведущее колесо отстающей (правой) гусеницы сможет вращаться с более высокой скоростью, допустим 300 об/мин (15 км/час). Поскольку скорость забегающей гусеницы осталась прежней, радиус поворота увеличится.
Для упрощения примем, что тормозная сила при этом не меняется (хотя в действительности при увеличении радиуса поворота она становится меньше). Тогда величина крутящего момента, передаваемого через фрикцион, не изменится, несмотря на пробуксовку фрикциона. Поскольку скорость отстающей гусеницы увеличилась в 1,5 раза, мощность, отдаваемая ее ведущим колесом, возрастет также в 1,5 раза и вместо 50 л. с. достигнет 75 л, с.
Передаточное число коробки равно 10. Значит, ведомый вал фрикциона, расположенный перед коробкой, всегда вращается в 10 раз быстрее, чем ведущее колесо, установленное за коробкой, и при 300 оборотах ведущего колеса будет делать 3000 об/мин. Ведущий же вал фрикциона, связанный с двигателем, как и раньше, делает 2000 об/мин. Крутящий момент, передаваемый фрикционом, также не изменился, так как тормозная сила осталась прежней. Значит, мощность, передаваемая забегающей гусенице, не изменится — она останется равной 50 л. с. Между тем к фрикциону подводится мощность 75 л. с. 25 л. с. затрачивается на преодоление трения между дисками фрикциона, т. е. превращается в тепло.
Если к забегающей гусенице требуется подвести 150 л. с., а отстающая дает 50 л. с, двигатель попрежнему должен развивать 100 л. с. Таким образом, с увеличением действительного радиуса поворота сравнительно с расчетным потребная мощность двигателя не изменилась.
Известно, что мощность внешних сопротивлений уменьшается с увеличением радиуса поворота. Оказывается, что если поворот сопровождается пробуксовкой фрикциона, то, кроме мощности внешних сопротивлений, для поворота необходима дополнительная мощность, затрачиваемая на трение во фрикционе. Эта мощность называется тормозной мощностью.
Теперь мощность, которую должен дать двигатель, или потребная мощность, уже не будет равна мощности внешних сопротивлений; к последней добавится тормозная мощность.
ПОВОРОТ С БУКСОВАНИЕМ ТОРМОЗА
Танк может повернуться с радиусом больше В и другим способом: при помощи остановочных тормозов, которые тормозят ведущие колеса танка. Выключим передачу в коробке отстающей гусеницы и будем затягивать остановочный тормоз. Если тормоз затянуть неполностью, ведущее колесо отстающей гусеницы будет вращаться. При этом радиус поворота зависит от степени затяжки тормоза.
Отстающая гусеница попрежнему отдает мощность, но теперь эта мощность не возвращается к забегающей гусенице: передача в коробке выключена, и связи между гусеницами нет. Мощность, возвращаемая отстающей гусеницей, полностью превращается в тормозе в тепло. Здесь происходит то же явление, которое наблюдалось в примере с электрической передачей, когда мощность генератора тратилась в реостате (см. рис. 488). Всю мощность, необходимую для забегающей гусеницы, должен дать двигатель; отстающая гусеница ему не помогает, циркуляции мощности нет.
Сравним поворот с одним и тем же радиусом R=10Вв двух случаях: в первом, когда происходит циркуляция мощности, т. е. включены разные передачи коробок и поворот совершается с пробуксовкой фрикциона (пусть расчетный радиус Rр = 5В); во втором, когда нет циркуляции мощности, т. е. передача одной коробки выключена и поворот совершается с буксованием тормоза (расчетный радиус Rр= В).
На рис, 491 показана передача мощности через механизмы танка при повороте с циркуляцией мощности, т. е. при повороте с пробуксовкой фрикциона.
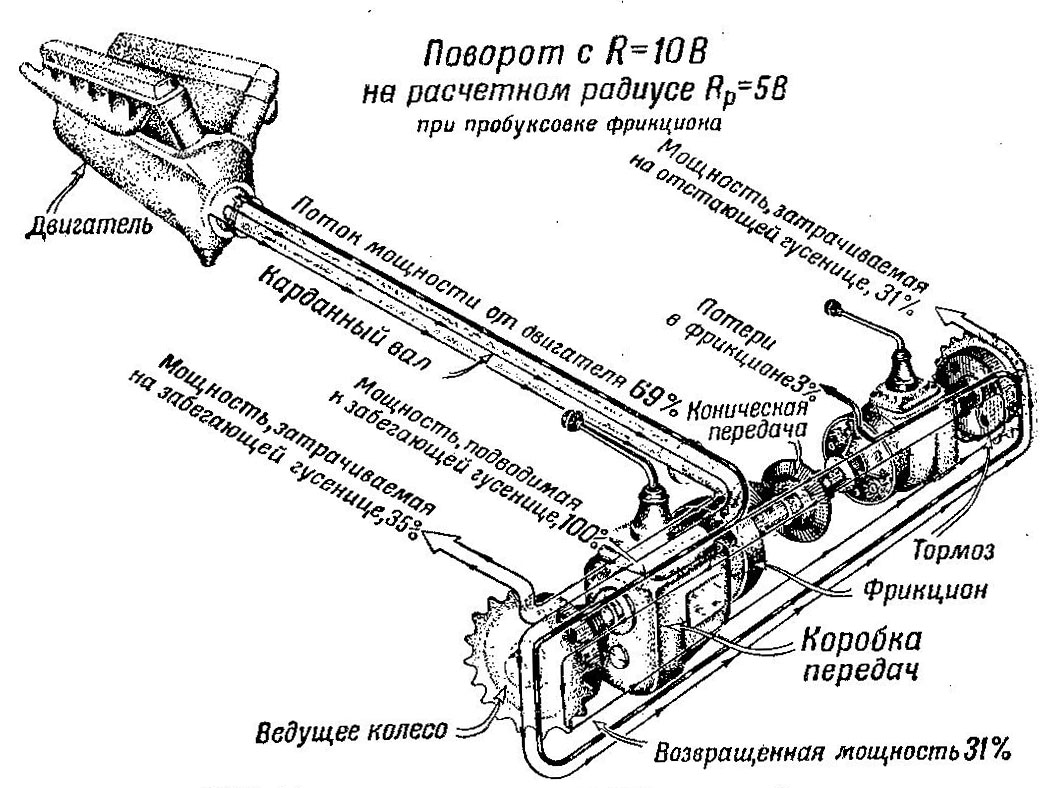
Рис. 491 Передача мощности при повороте в трансмиссии с бортовыми коробкамипередач
На рис. 492 приведена диаграмма передачи мощности для этого случая.
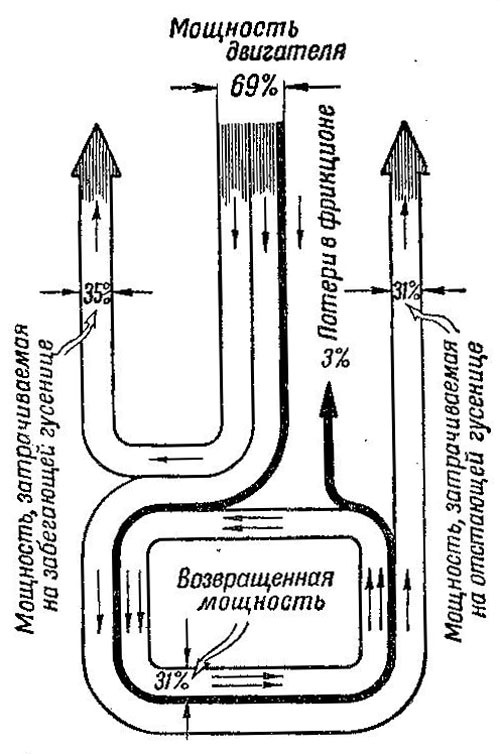
Рис. 492 Диаграмма расхода мощности цри повороте с радиусомR= 10 В на расчетном радиусе Rр— 5 В при пробуксовке фрикциона
Как видно из рисунка, мощность, идущая от двигателя, передается забегающей гусенице; к ней прибавляется мощность, возвращаемая отстающей гусеницей. Если принять всю мощность, посту пающую к забегающей гусенице, за 100%, то от двигателя будет поступать 69%, а от отстающей гусеницы 31% (см. диаграмму).
35% всей мощности, подведенной к забегающей гусенице, будет затрачено этой гусеницей на преодоление сопротивления грунта; вся остальная мощность (65%) перейдет к отстающей гусенице, где 31% (на 4% меньше, чем на забегающей гусенице, так как скорость отстающей гусеницы меньше) затрачивается на преодоление сопротивления грунта; 31% вернется через коробки к забегающей гусенице, а 3% мощности будут затрачены на трение во фрикционе. Мощность, расходуемая на трение, показана на рис. 491 и на диаграмме в виде жирной линии.
Поворот с выключенной передачей и пробуксовкой тормоза при Rр = В иллюстрируется диаграммой рис. 493.

Рис. 493 Диаграмма расхода мощности при повороте с радиусом R = 10 В на расчетном радиусе Rр = В при пробуксовке тормоза
В этом случае вся мощность (100%), идущая к забегающей гусенице, поступает от двигателя, так как циркуляции мощности нет. По-прежнему 35% этой мощности тратится забегающей гусеницей на преодоление сопротивления грунта, а остальная мощность идет к отстающей гусенице. 31% тратится на преодоление сопротивления, а 34%, т. е. более одной трети всей мощности, ввиду не возможности вернуться к забегающей гусенице затрачиваются на трение в тормозе. Мощность, идущая в тормоз, показацна на диаграмме темной полосой.
Таким образом, поворот без циркуляции мощности невыгоден по двум причинам; во-первых, от двигателя требуется значительно, большая мощность, а если он не в состоянии ее развить, придется уменьшить скорость танка; во-вторых, потеря мощности на трение в рассматриваемом примере более чем в 10 раз превышает ту же потерю в первом случае. Это значит, что тормоз будет нагреваться очень сильно и изнашиваться во много раз быстрее, чем фрикцион при повороте с циркуляцией мощности.
ТОРМОЗНАЯ И ПОТРЕБНАЯ МОЩНОСТЬ ПРИ РАЗЛИЧНЫХ РАСЧЕТНЫХ РАДИУСАХ
Как уже было указано, потребная для поворота мощность двигателя (обозначим ее через Nп) складывается из двух мощностей: мощности внешних сопротивлений Nо и тормозной Nт, или
Nп = Nо + Nт
Мощность внешних сопротивлений определяется сопротивлением грунта, радиусом поворота и скоростью забегающей гусеницы. Она не зависит от устройства механизма поворота. Иначе обстоит дело с тормозной мощностью.
Величина тормозной мощности зависит от того, какая часть мощности, возвращаемой отстающей гусеницей, может перейти на забегающую, т. е. зависит от циркуляции мощности. При повороте с пробуксовкой тормоза, когда расчетный радиус равен ширине колеи танка, а действительный радиус поворота превосходит расчетный (R больше В), циркуляции нет; вся мощность, идущая от отстающей гусеницы, поглощается тормозом. В этом случае двигатель должен развивать значительно большую мощность, чем при наличии циркуляции.
На рис. 494 показано, как при отсутствия циркуляции изменяется потребная мощность двигателя в зависимости от радиуса поворота при расчетном радиусе Rр = В.

Рис. 494 Изменение потребной удельной мощности двигателя в зависимости от радиуса поворота при отсутствии циркуляции мощности
Расчетный радиус Rр= В, v2 — 1 км/час.
Показана потеря мощности в тормозе {заштрихованная часть)
Как и раньше, на графике приводится удельная мощность при скорости забегающей гусеницы v2= 1 км/час. Нижняя кривая показывает мощность внешних сопротивлений, верхняя — потребную мощность. Тормозная мощность равна разности между потребной мощностью и мощностью внешних сопротивлений, а потому ее можно определить для любого радиуса по расстоянию между кривыми (заштрихованная часть диаграммы).
Из графика следует, что наибольшая тормозная мощность затрачивается при радиусе поворота, равном 3В. Так, при весе танка 30 ти скорости 10 км/час эта мощность будет равна 0,55 х 30 х 10 = 165 л. с.
Тормозная мощность составляет в этом случае около 85% мощности внешних сопротивлений.
Картина резко меняются, если механизм поворота обеспечивает циркуляцию мощности.
Пусть мехаешм поворота имеет при расчетных радиуса:
Rр1= В; Rр2= 2В ; Rр3= 4В.
Такой механизм поворота называется трехступенчатым по числу расчетных радиусов.
Примером такого механизма могут служить трехступенчатые бортовые коробки. Так, комбинация «нейтраль» — третья передача (с торможением гусеницы) дает Rр1= В, первая передача — третья дает Rр2= 2В , вторая передача — третья дает Rр3=4В (считаем, что комбинация первой передачи со второй не используется).
Поворот с радиусом от В до 2В происходит лишъна первой ступени Rр1= В и сопровождается пробуксовкой тормоза (рис. 495).
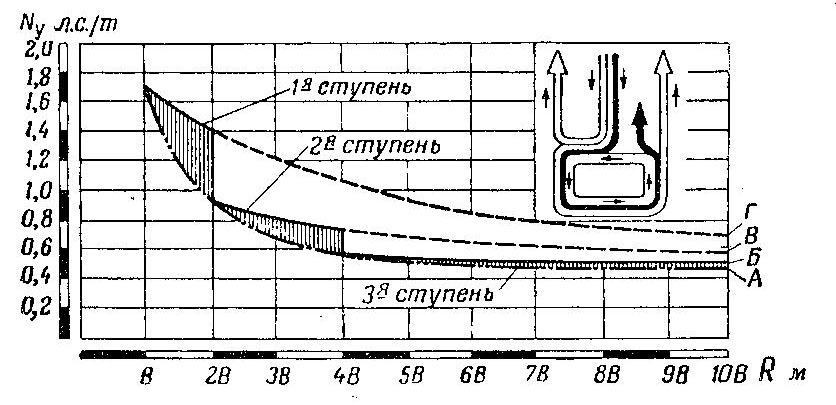
Рис. 495 Изменение потребной удельной мощности двигателя при циркуляции мощности (танк с трехступенчатым механизмом поворота)
Циркуляции мощности не будет; расход мощности такой же, как только что разобранном нами случае. Но уже для радиуса 2Bможно перейти на вторую ступень, включивво второй коробке первую передачу. При повороте с радиусом 2В, который является расчетным дляданной ступени, тормозная мощность равна нулю, так как фрикцион не пробуксовывает. Потребная мощность двигателя будет равна мощности внешних сопротивлений, ввиду того что вся мощность, возвращаемая отстающей гусеницейг переходит на забегающую, т, е. происходит полная циркуляция мощности.
Поворот на радиусах от 2В до 4В происходит на второй ступени при пробуксовке фрикциона отстающей гусеницы. Тормозная мощность в этом случае невелика, так как к здесь происходит циркуляция мощности. На радиусе 4В можно переходить на третью ступень, включив для этого во второй коробке вторую передачу. Увеличение циркуляции мощности приводит к тому, что на последующих радиусах поворота тормозная мощность вновь значительно падает.
Расход мощности при повороте с трехступенчатым механизмом показан на рис. 495. Заштрихованные участки соответствуют тормозной мощности. Для действительного радиуса поворота 10В приведены три величины тормозной мощности: для поворота на первой ступени (отрезок АГ), на второй (АВ) и на третьей (АБ). Сравнивая эти величины, видим, что при переходе на вторую ступень тормозная мощность уменьшается вдвое, а при переходе на третью — еще в 3 раза. Это достигается благодаря циркуляции мощности.
Из рис. 495 следует еще один вывод: наиболее значительную экономию мощности дает переход на вторую ступень (Rр= 2В), несколько меньшую — переход на третью ступень (Rр= 4В). Если ввести в механизм четвертую ступень с расчетным радиусом, скажем, 5—6B, это даст совершенно ничтожную экономию мощности.
Таким образом, требованиям в отношении расхода мощности вполне будет удовлетворять трехступенчатый механизм с расчетными радиусами В, 2В, 3—4B. Двухступенчатый механизм, обеспечивающий повороты с расчетными радиусами В и 3—4B, дает увеличенный расход мощности только на малых радиусах (между Rр1и Rр2).
Однако поворот на таких радиусах возможен лишь при небольших скоростях, (при которых двигатель имеет достаточный запас мощности. Поэтому вполне можно примириться в этими потерями и, чтобы не усложнять механизм поворота, ограничиться двумя ступенями, т. е. двумя расчетными радиусами.
МЕХАНИЗМЫ ПОВОРОТА
Все механизмы поворота танков могут быть разделены на две группы.
К первой принадлежат механизмы, у которых изменение скорости одной гусеницы не вызывает обязательного изменения скорости другой. Такие механизмы называют независимыми. К ним относятся рассмотренные нами бортовые коробки передач, планетарные механизмы поворота и бортовые фрикционы.
Ко второй группе относятся механизмы, у которых изменение скорости одной гусеницы обязательно вызывает изменение скорости другой. Эти механизмы называют дифференциальными. При таких механизмах уменьшение скорости отстающей гусеницы вызывает увеличение скорости забегающей. К ним относятся простой и двойной дифференциалы.
Рассмотрим наиболее часто встречающиеся механизмы поворота обеих групп.
НЕЗАВИСИМЫЕ МЕХАНИЗМЫ
БОРТОВЫЕ ФРИКЦИОНЫ
Если в схеме трансмиссии (см. рис. 491) заменить две коробки передач одной, служащей для прямолинейного движения, то механизмами гюворота могут служить два фрикциона и два тормоза. Фрикцион в этом случае называется бортовым. Схема трансмиссии с бортовыми фрикционами показана на рис. 496.
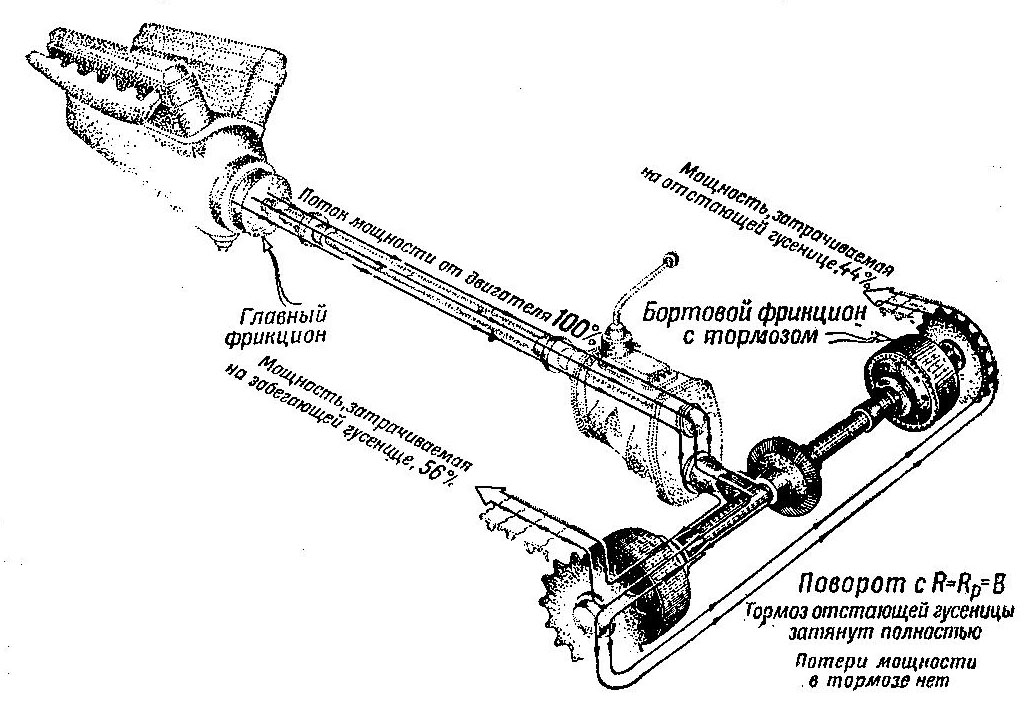
Рис. 496 Схема трансмиссии с бортовыми фрикционами
Схема бортового фрикциона показана на рис. 497 (его устройство было рассмотрено в главе III).
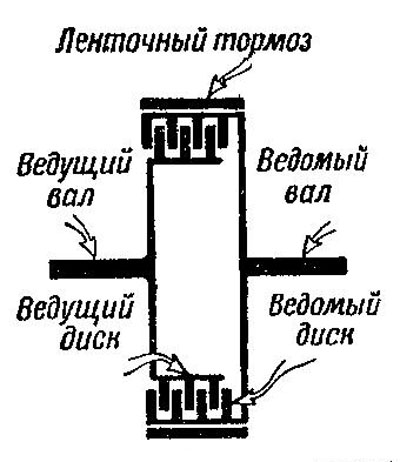
Рис. 497 Схема бортового фрикциона
При прямолинейном движении оба фрикциона включены, а оба тормоза отпущены. Для поворота один из фрикционов выключается. Поворот в этом случае не произойдет, точнее — он будет происходить с весьма большим радиусом. Чтобы танк повернулся, необходимо, выключив фрикцион, затянуть тормоз.
Расчетный радиус поворота у танка с бортовыми фрикционами один; он равен ширине колеи танка; поворот на таком радиусе происходит, когда тормоз полностью затянут (см. рис. 496).
Поворот с радиусом, большим В, происходит при пробуксовке тормоза. Как показано на диаграмме (см, рис. 493), вся мощность двигателя поступает через включенный фрикцион на забегающую гусеницу. Мощность от отстающей гусеницы не может вернуться к забегающей, так как фрикцион выключен, и расходуется в тормозе. При R= 10Bдля при пятых нами условий мощность, теряемая в тормозе, составляет 34% всей мощности двигателя, а 31% мощности, поступившей на отстающую гусеницу, затрачивается ею на преодоление внешних сопротивлений.
Таким образом, бортовой фрикцион служит только для отключения ведущего колеса отстающей гусеницы от двигателя, а радиус поворота меняется путем изменения затяжки тормоза, поэтому устойчивость поворота на всех радиусах, кроме расчетного, не обеспечивается.
Бортовой фрикцион является несовершенным механизмом поворота, так как обеспечивает только один расчетный радиус, Кроме того, подобно всем фрикционным механизмам, бортовой фрикцион требует частой регулировки.
ПЛАНЕТАРНЫЕ МЕХАНИЗМЫ ПОВОРОТА
Планетарные коробки передач могут служить механизмами поворота, если на каждый борт танка поставить по одной коробке (рис. 498); при этом отпадает необходимость в фрикционах, поскольку роль фрикциона в планетарной передаче выполняет тормоз.
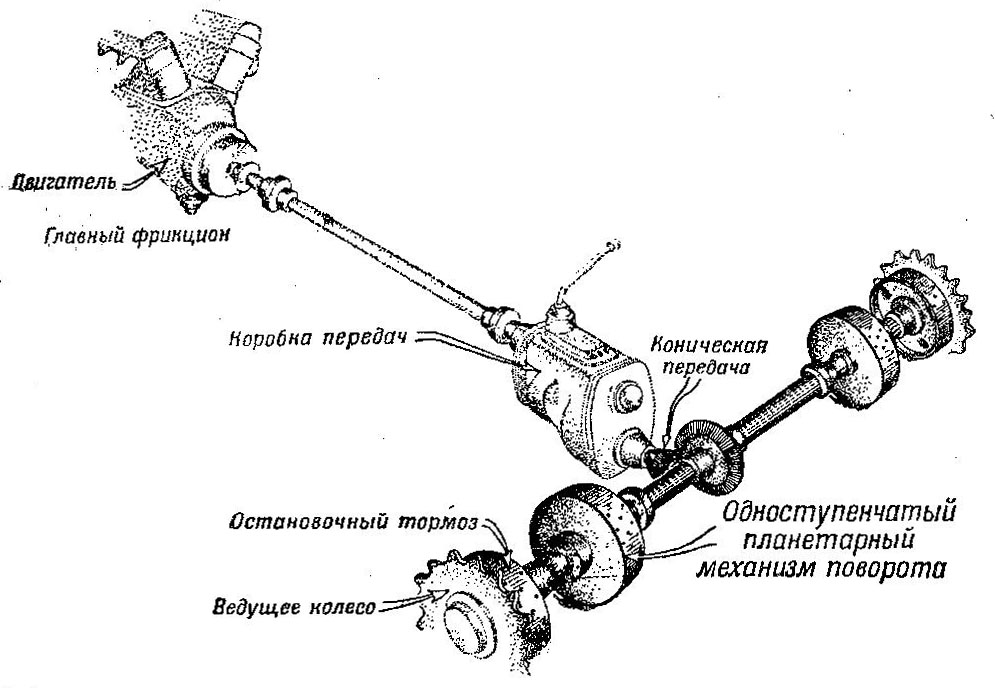
Рис. 498 Схема трансмиссии с одноступенчатыми планетарными механизмами поворота
Планетарные механизмы поворота могут быть одноступенчатыми (с одним расчетным радиусом) и многоступенчатыми (со многими расчетными радиусами).
Схема одноступенчатого планетарного механизма показана на рис. 499, а его устройство — на рис. 500.
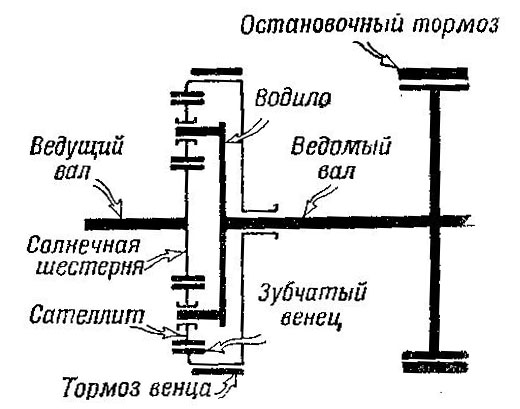
Рис. 499 Схема одноступенчатого планетарного механизма поворота
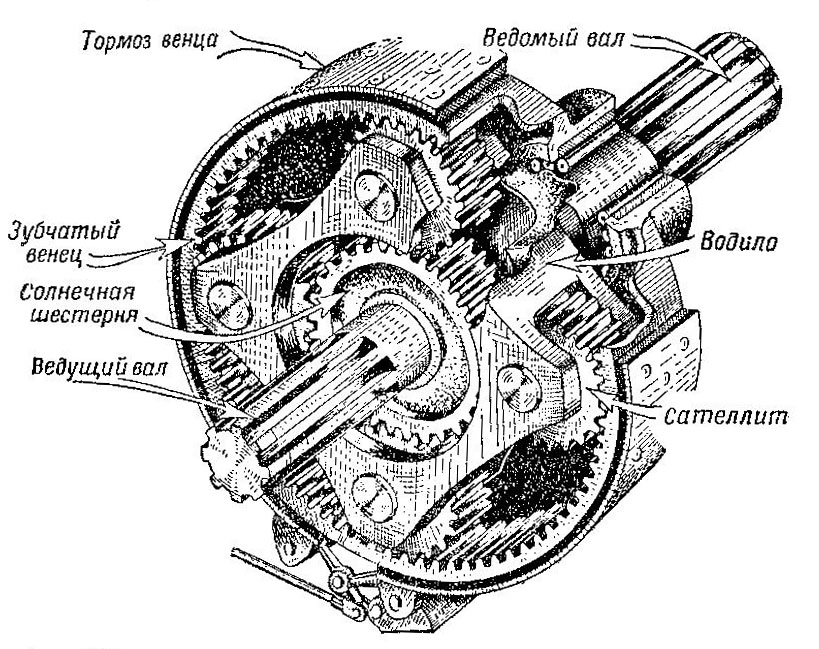
Рис. 500 Устройство одноступенчатого планетарного механизма. Остановочный тормоз снят с ведомою вала
Одноступенчатый планетарный механизм состоит из уже знакомых нам деталей: солнечной шестерни, сателлитов, водила и зубчатого венца с тормозом. Солнечные шестерни левого и правого планетарных механизмов поворота установлены на ведущем валу этих механизмов, который одновременно служит поперечным валом конической передачи трансмиссии танка. Водило планетарного механизма через ведомый вал соединено с ведущим колесом танка. На ведомом валу установлен остановочный тормоз.
При прямолинейном движе-нии оба тормоза венцов планетарных механизмов затянуты, а оба остановочных тормоза отпущены; при этом ведомые валы планетарных механизмов вращаются с одинаковым числом оборотов, но медленнее ведущих (вследствие обкатывания сателлитов по неподвижному венцу). Для поворота необходимо отпустить тормоз венца планетарного механизма и затянуть остановочный тормоз; это соответствует выключению передачи бортовой коробки. Расчетный радиус поворота один, он равен ширине колеи танка (Rр=B) как у танка с бортовыми фрикционами. Увеличение радиуса достигается пробуксовкой остановочного тормоза.
По поворотливости танк с одноступенчатыми планетарными механизмами поворота ничем не отличается от танка с бортовыми фрикционами и обладает теми же недостатками в отношении расхода мощности и устойчивости поворота, что и бортовой фрикцион. Главное преимущество его — большая надежность в работе. Регулировать его приходится реже, чем бортовой фрикцион. Кроме того, для затяжки тормоза венца требуется меньшая сила, чем для выключения фрикциона; зато затягивать остановочный тормоз тяжелее (на его валу момент больше, чем у такого же танка с бортовыми фрикционами).
Многоступенчатые планетарные механизмы состоят из двух планетарных коробок передач с несколькими передачами в каждой. На ведомом валу коробки ставится остановочный тормоз.
Многоступенчатые планетарные механизмы работают так же, как бортовые коробки передач. При прямолинейном движении включены одинаковые передачи обеих планетарных коробок. Для поворота выключается высшая передача коробки отстающей гусеницы и включается низшая, т. е. отпускается тормоз высшей передачи и затягивается тормоз низшей.
Число расчетных радиусов зависит от числа передач коробки. Наименьший расчетный радиус обычно равен ширине колеи; для поворота с таким радиусом выключают все передачи коробки отстающей гусеницы и затягивают остановочный тормоз. Поворот на промежуточных радиусах сопровождается пробуксовкой остановочного тормоза, или тормоза одной из планетарных передач, заменяющего фрикцион бортовой коробки.
Применяемые на танках двухступенчатые планетарные механизмы имеют две передачи в каждой бортовой коробке. Двух передач для прямолинейного движения танка мало, поэтому нельзя обойтись без главной коробки передач, используемой в этом случае только для прямолинейного движения. Однако число передач главной коробки можно уменьшить, так как двухступенчатый механизм поворота при прямолинейном движении может работать в качестве демультипликатора.
Двухступенчатый механизм дает два расчетных радиуса: Rр = B—при нейтрали и затянутом остановочном тормозе и Rр2 > В— при включенной высшей передаче одной коробки и низшей — другой.
Чтобы упростить двухступенчатый планетарный механизм, второй планетарный ряд иногда заменяют фрикционом. Схемы такого механизма показаны на рис. 501 и 502, устройство его было рассмотрено в главе Ш.
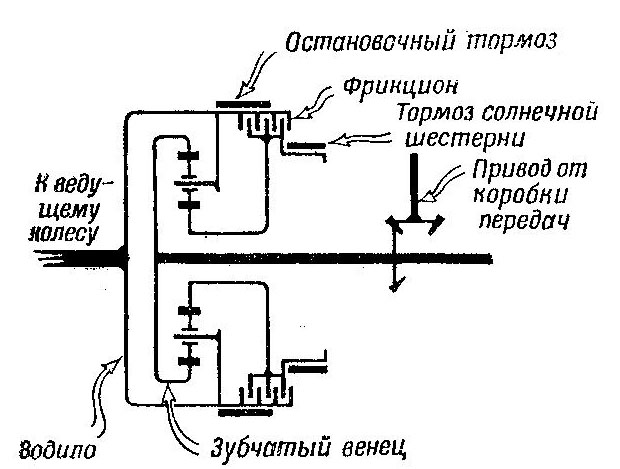
Рис. 501 Принципиальная схема двухступенчатого планетарного механизма поворота
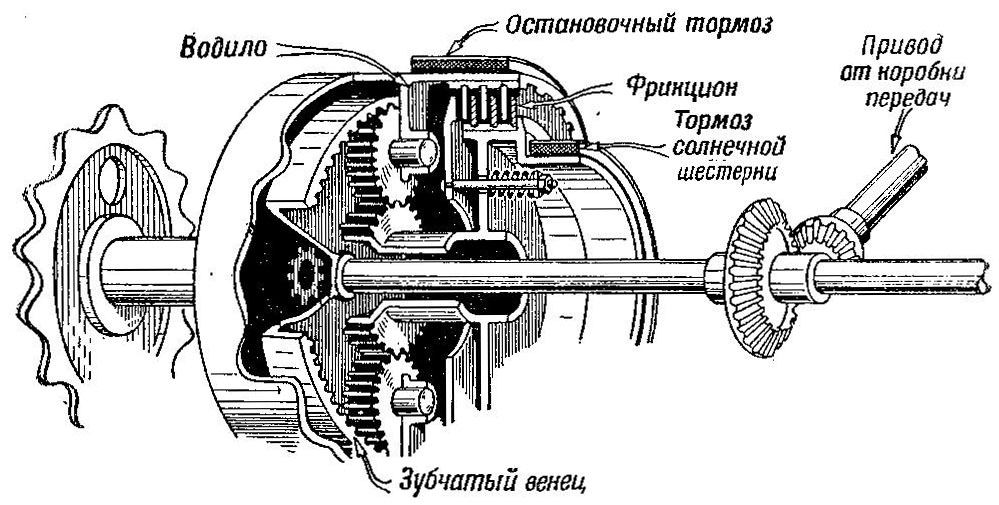
Рис. 502 Конструктивная схема двухступенчатого планетарного механизма поворота
Рассмотрим работу двухступенчатого планетарного механизма поворота в случае, когда оба тормоза—солнечной шестерни и остановочный — отпущены, а фрикцион включен. При включенном фрикционе солнечная шестерня соединена с водилом и, следовательно, может вращаться только в ту же сторону и с тем же числом оборотов, что и водило.
Будем вращать венец по часовой стрелке. Если сателлит начнет вращаться на своей оси, он будет вращать солнечную шестерню против часовой стрелки. В этом случае водило, связанное с солнечной шестерней, также должно повернуться в ту же сторону, т. е. в сторону, противоположную направлению вращения венца. Однако это невозможно. Вспомним пример с рычагом, заменяющим сателлит. Если поворачивать рычаг за один конец, его ось может либо оставаться неподвижной, либо перемещаться в ту же сторону. Следовательно, повернуть сателлит на оси не удастся.
Поскольку сателлит не может вращаться на своей оси, то, действуя на его зуб (вращая венец), мы заставим водило, а с ним и солнечную шестерню вращаться в ту же сторону и с тем же числом оборотов, с каким вращается венец. Сателлит не обегает вокруг солнечной шестерни, а увлекает как ее, так и водило; вся передача вращается как одно целое; передаточное число i= 1.
Условия работы фрикциона планетарной передачи значительно легче, чем обычного бортового фрикциона. Бортовой фрикцион передает весь крутящий момент, передаваемый к ведущему колесу, тогда как фрикцион планетарной передачи передает лишь небольшую часть крутящего момента; большая часть его передается непосредственно через ось сателлита на водило. Поэтому фрикцион значительно меньше бортового, и диски его изнашиваются меньше. Следовательно, работает он гораздо надежнее.
Если выключить фрикцион и затянуть тормоз солнечной шестерни, остановив ее, сателлиты начнут вращаться на своих осях, обегая неподвижную солнечную шестерню. Механизм будет работать, как обычный планетарный, причем водило будет вращаться медленнее венца (iбольше единицы).
Наконец, если отпустить тормоз солнечной шестерни и затянуть остановочный тормоз, планетарная передача будет выключена, а отстающая гусеница заторможена.
Управление танком осуществляется следующим образом. При прямолинейном движении на обо>их бортах включена высшая передача (включены оба фрикциона). Для поворота с большим радиусом фрикцион на одном борту выключают, после чего затягивают тормоз солнечной шестерни. Различные радиусы поворота получаются в результате пробуксовки этого тормоза. При полной затяжке тормоза отстающая гусеница вращается — расчетный радиус будет больше В (обычно 3—4 В). Наконец, для крутого поворота тормоз солнечной шестерни отпускают и, не включая фрикцион, затягивают остановочный тормоз. При полностью затянутом тормозе отстающая гусеница неподвижна, расчетный радиус равен В.
Двухступенчатый механизм обеспечивает более устойчивый поворот, чем бортовой фрикцион. Действительно, при полностью затянутом тормозе солнечной шестерни поворот танка будет происходить с вполне определенным расчетным радиусом. При пробуксовке этого тормоза радиус поворота может меняться, но он никогда не будет меньше расчетного на второй передаче (3—4 В), в то время как у танка с бортовыми фрикционами радиус поворота может меняться в более широких пределах — до радиуса, равного ширине колеи.
ДИФФЕРЕНЦИАЛЬНЫЕ МЕХАНИЗМЫ
ПРОСТОЙ ДИФФЕРЕНЦИАЛ
Схема трансмиссии с простым дифференциалом показана на рис. 503.
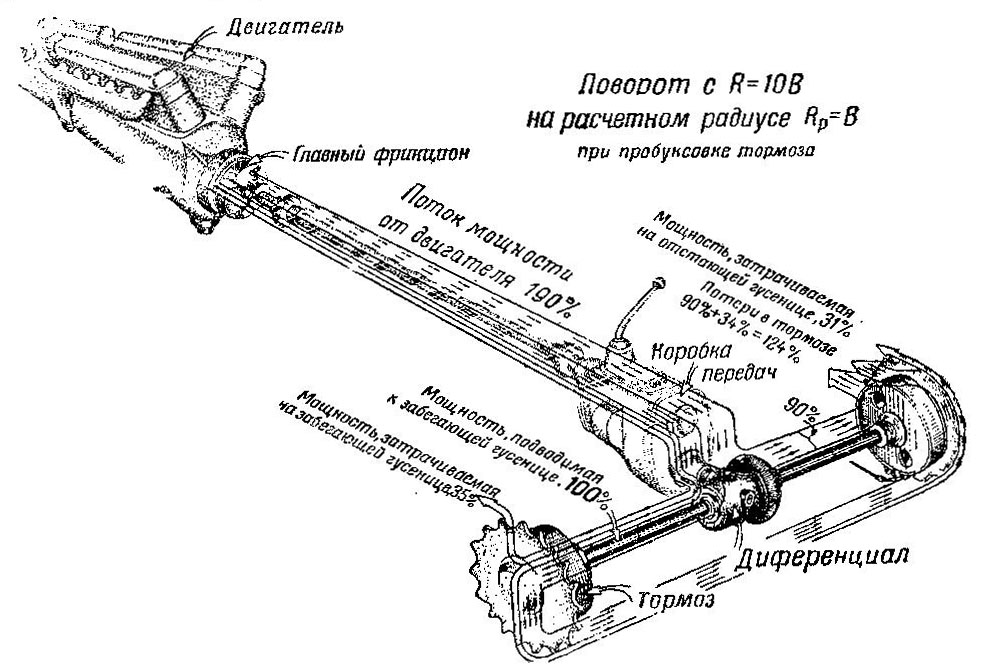
Рис. 503 Схема трансмиссии с простым дифференциалом
В зависимости от устройства различают дифференциалы конические и цилиндрические.
На рис. 504 показана схема конического дифференциала, а на рис. 505 — его устройство.

Рис. 504 Схема простого конического дифференциала

Рис. 505 Устройство простого конического дифференциала
Дифференциал представляет собой планетарный механизм. Его водило, называемое обычно коробкой сателлитов, связано через коническую передачу с ведомым валом коробки передач. Каждый сателлит сцеплен с двумя шестернями полуосей (солнечными шестернями). Одна из них соединена полуосью с правым, другая с левым ведущим колесомтанка. На полуосях поставлены тормоза (см. рис. 503).
Чтобы понять, как работает дифференциал, представим себе, что сателлиты в нем заменены рычажками (рис. 506, А и Б).
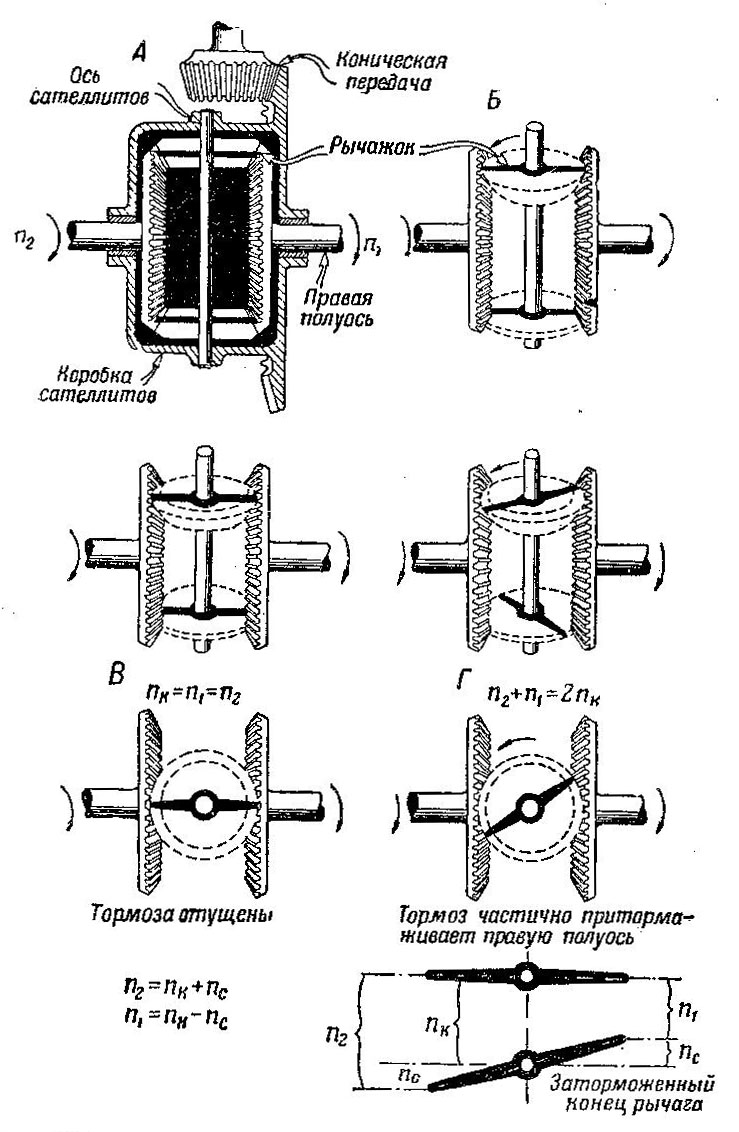
Рис. 506 Схема работы простого конического дифференциала
Рычажок средней частью установлен на оси, закрепленной в коробке сателлитов, а концы его находятся между зубьями полуосевых шестерен.
Пусть сопротивление движению обеих гусениц одинаково и тормоза на полуосях отпущены (рис. 506, В). Тогда, чтобы повернуть каждую из шестерен полуосей, требуется одинаковая сила. Если начать вращать коробку сателлитов, рычажок, середина которого-перемещается вместе с коробкой, увлечет обе шестерни полуосей.
Если танк движется по ровной дороге и на обеих гусеницах сопротивления одинаковы, коробка сателлитов, полуосевые шестерки и сателлиты вращаются как одно целое.
Если обозначить число оборотов коробки сателлитов через nk а число оборотов полуосей n2 и n1 то в этом случае
n2 = n1= nk
Затянем частично тормоз одной полуоси так, чтобы он мог пробуксовать (рис. 506, Г). Тогда ведущее колесо этой полуоси начнет отставать. Вместе с ним будет отставать шестерня полуоси и связанный с нею конец рычажка. Рычажок начнет поворачиваться на своей оси. Ввиду того что середина рычажка перемещается вместе с коробкой сателлитов, заторможенный конец его будет отставать от середины, а свободный обгонять ее.
Пусть середина рычажка переместилась на расстояние пк (рис. 506, схема внизу). Заторможенный конец рычажка отстанет от середины на величину пс и пройдет расстояние п1 = пк — пс. Рассматривая рисунок, нетрудно убедиться, что второй конец рычажка всегда будет обгонять середину на столько, на сколько отстает первый, т. е, на величину пс; значит, второй конец пройдет путь п2 = пк + пс. Отсюда следует, что связанная со свободным концом рычажка шестерня полуоси будет подгоняться им и вращаться быстрее коробки: п2 > пк , а вторая (заторможенная) будет задерживаться и вращаться медленнее коробки: п1 < пк.
От рычажка нетрудно перейти к сателлиту. В данном случае сателлит будет вращаться на своей оси, задерживая одну шестерню и подгоняя другую. Если коробка сателлитов сделает nк об/мин, то одна полуось (забегающая) будет делать n2 = nк + ncоб/мин, а другая (отстающая) n1 = nк — nсоб/мин, т. е. на сколько увеличится число оборотов забегающей полуоси, на столько уменьшится число оборотов отстающей.
Сложим числа оборотов забегающей и отстающей гусениц:
n2+ n1 = nк + nс + nк - nс
или
n2 + n1 = 2 nк
Отсюда видно, что, как бы ни изменялось число оборотов полуосей, сумма их всегда останется одной и той же, если обороты двигателя постоянны; она равна удвоенному числу оборотов коробки сателлитов.
Когда одна из полуосей, допустим первая, заторможена полностью, она не вращается, т. е. ее обороты n1 = 0; тогда n2 + 0 = 2nк или n2 = 2nк, Следовательно, при полном торможении одной полуоси вторая полуось вращается вдвое быстрее коробки сателлитов.
Рассмотрим управление танка с дифференциалом.
Если сопротивление движению обеих гусениц одинаково и тормоза не затянуты, сателлиты не будут вращаться на своих осях и, следовательно, обе шестерни полуосей будут делать одинаковое число оборотов, равное числу оборотов коробки сателлитов. Танк будет двигаться прямолинейно.
Чтобы повернуть танк, надо затянуть тормоз с той стороны, в которую нужно повернуться. Сателлиты начнут вращаться на своих осях, причем шестерня полуоси, связанная с отстающей гусеницей, будет вращаться медленнее, чем в случае прямолинейного движения танка, а связанная с забегающей быстрее. Скорости гусениц станут неодинаковыми, и танк начнет поворачиваться.
Здесь выясняется одно отрицательное свойство дифференциала. При повороте необходимо, чтобы скорость отстающей гусеницы уменьшилась. Но увеличение скорости забегающей гусеницы не является необходимостью; наоборот, оно нежелательно. Мощность, нужная для поворота, значительно превышает мощность прямолинейного движения. Из-за этого перед поворотом часто приходится переходить на низшую передачу, чтобы двигатель не заглох. Дифференциал же повышает скорость забегающей гусеницы, что еще более увеличивает нагрузку на двигатель.
Чем сильнее затянут тормоз, т. е. чем круче поворот, тем больше увеличивается скорость забегающей гусеницы, в то время как на крутых поворотах нагрузка на двигатель и без того весьма велика.
При полностью затянутом тормозе отстающая гусеница остановится, я забегающая станет вращаться вдвое быстрее, чем при прямолинейном движении (конечно, если число оборотов двигателя и передача коробки останутся прежними). В данном случае танк будет поворачиваться с расчетным радиусом Rр = В; при этом вся мощность двигателя расходуется на внешние сопротивления, так как в тормозе мощность не расходуется (тормозной барабан не вращается). Поворот на всех остальных радиусах сопровождается пробуксовкой тормоза.
На рис. 503 показано распределение мощности при повороте танка с простым дифференциалом. Для сравнения с другими механизмами, рассмотренными нами выше, взят тот же радиус поворота (R= 10 В) и та же скорость забегающей гусеницы. Мощность, подводимая к забегающей гусенице, как и ранее, принята за 100%. Вся эта мощность подводится от двигателя; циркуляции мощности нет, так как на пути возвращаемой мощности, на полуоси, стоит тормоз, и вся идущая от отстающей гусеницы мощность будет затрачена на трение в этом тормозе.
Как мы уже говорили, мощность внешних сопротивлений не зависит от того, какой механизм поворота установлен на танке. Поэтому из 100% мощности, подведенной к забегающей гусенице, как и в предыдущем случае, 35% будут израсходованы на этой гусенице на преодоление сопротивления грунта, а остальная мощность пойдет на отстающую гусеницу. Из этой мощности на внешние сопротивления затратится 31 % мощности, а 34% будут переданы отстающей гусеницей тормозу и израсходуются в нем.
До сих пор никаких отличий в расходе мощности у простого дифференциала по сравнению с бортовым фрикционом и другими механизмами, работающими без циркуляции, мы не обнаружили. Но при повороте танка с бортовыми фрикционами один из них выключался, и тормозной барабан оказывался отключенным от двигателя. Поэтому приходилось удерживать тормозом только отстающую гусеницу, не давая ей увеличивать скорость. Дифференциал же сохраняет связь двигателя с тормозным барабаном. Двигатель стремится вращать отстающую полуось с той же скоростью, с какой он вращает забегающую. В силу этого часть мощности передается от двигателя через шестерни дифференциала на отстающую полуось. Эта мощность также расходуется в тормозе, так как для поворота она не нужна. Таким образом, мощность к тормозу подводится с двух сторон.
Для R= 10Bмощность, подводимая от двигателя к тормозу отстающей гусеницы, составляет 90% мощности на забегающей гусенице. Таким образом, от двигателя требуется почти удвоенная мощность (190%), причем две трети этой мощности тратятся в тормозе (см. рис, 503). Потеря мощности в тормозах танка с простым дифференциалом будет почти вчетверо больше, чем в тормозах танка с бортовыми фрикционами, если скорости поворота одинаковы.
На рис. 507 показан цилиндрический дифференциал.
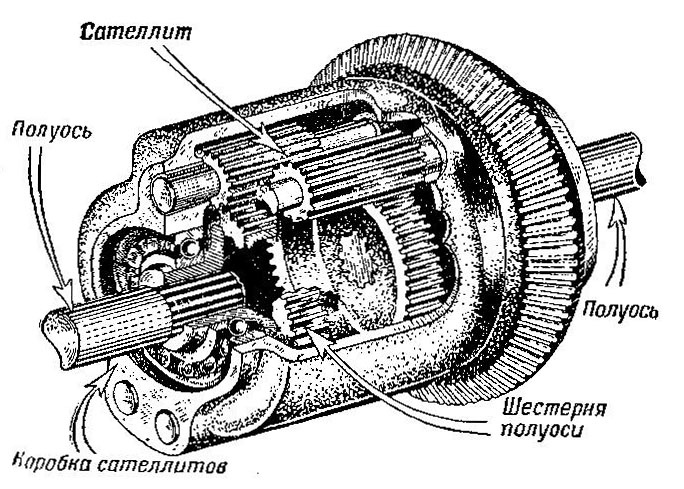
Рис.507 Устройство простого цилиндрического дифференциала
Конический и цилиндрический дифференциалы работают одинаково, но устройство их разное. В цилиндрическом дифференциале каждый сателлит связан с одной шестерней полуоси непосредственно, а с другой — через второй сателлит.
Если при неподвижной коробке сателлитов начать вращать одну полуось дифференциала, через сателлиты вращение будет передаваться другой полуоси. Эта полуось будет вращаться в обратную сторону; в этом легко убедиться, сравнивая рис. 505 и 507. Торможение одной полуоси вызывает ускоренное вращение другой полуоси в цилиндрическом дифференциале точно так же, как в коническом.
Дифференциал — очень простой механизм, не требующий особого ухода. Дифференциалы широко распространены на автомобилях, они хорошо освоены и дешевы в производстве; поэтому с точки зрения чисто производственной их выгодно использовать и на танках. Однако вследствие большого расхода мощности при повороте танка простой дифференциал вышел из употребления на танках, хотя в прошлом он применялся довольно часто, особенно на легких танках с большой удельной мощностью.
ДВОЙНОЙ ДИФФЕРЕНЦИАЛ
Двойные дифференциалы, так же как и простые, бывают конические и цилиндрические. На рис. 508 показана схема трансмиссии с двойным( коническим дифференциалом.
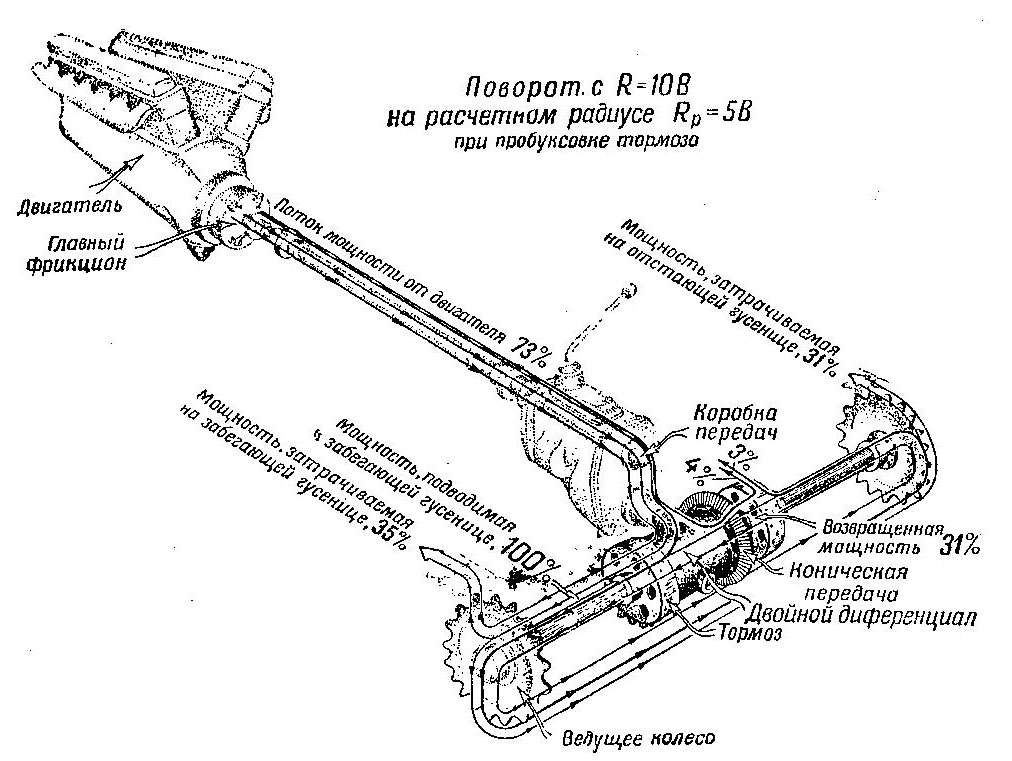
Рис. 508 Схема трансмиссии с двойным дифференциалом
Схема двойного конического дифференциала показана на рис, 509.
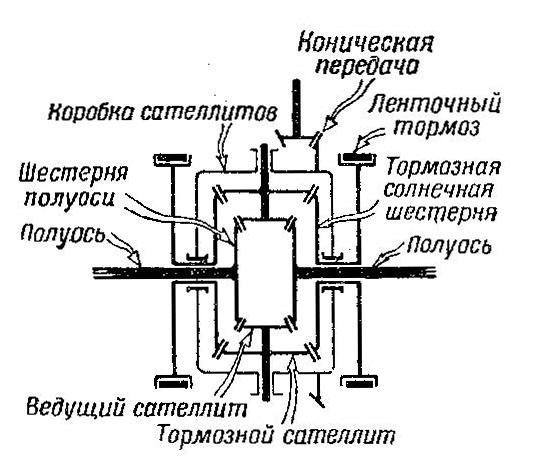
Рис. 509 Схема двойного коническогодифференциала
Двойной конический дифференциал (рис. 510), так же как и двойной цилиндрический (рис. 511), отличается от простого тем, что имеет с каждой стороны по две солнечные шестерни — шестерню полуоси и тормозную — и двойные сателлиты — ведущий и тормозной.
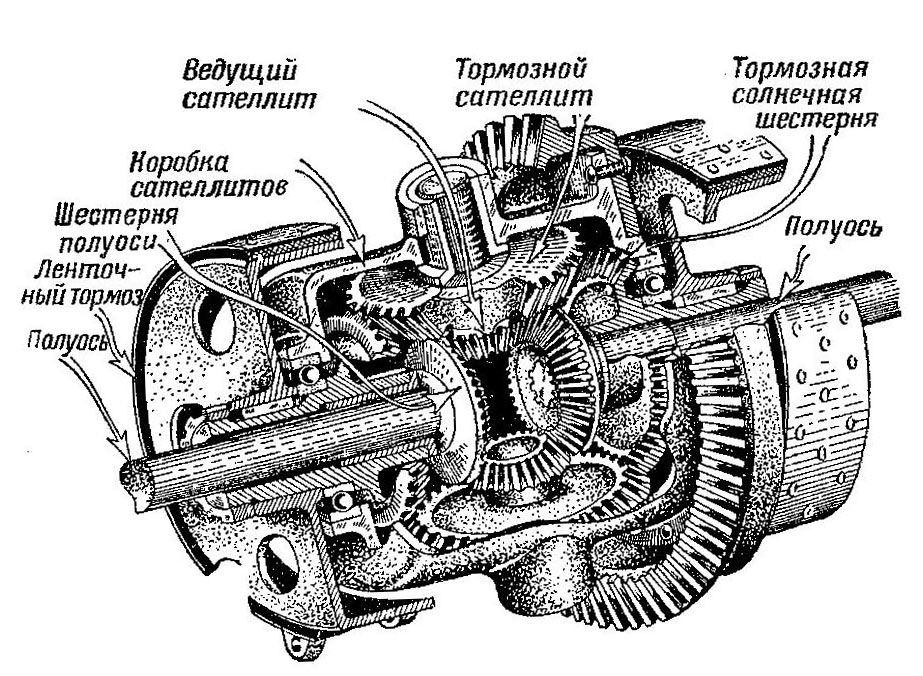
Рис. 510 Устройство двойного конического дифференциала
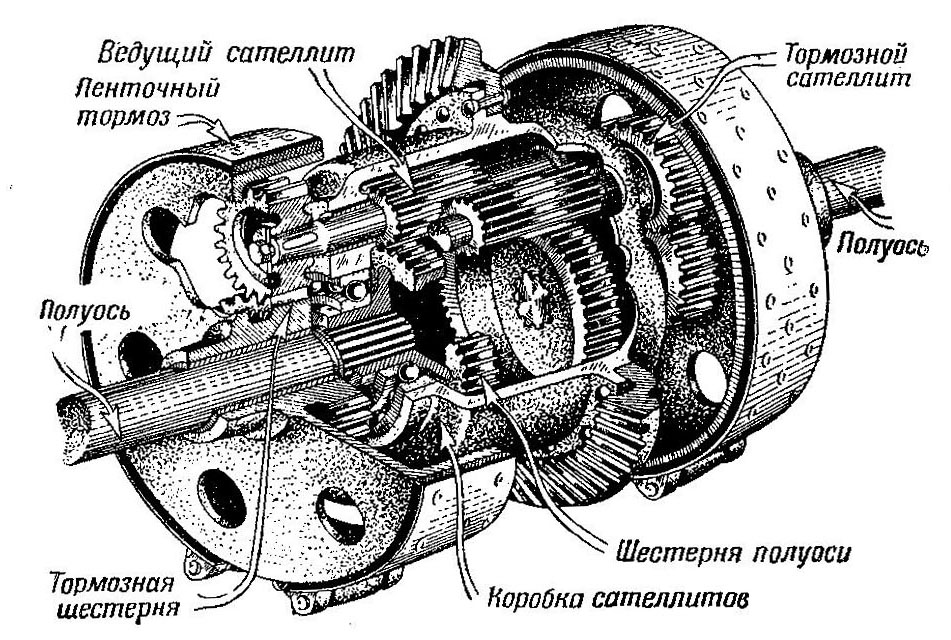
Рис. 511 Устройство двойного цилиндрического дифференциала
Отсюда и название двойной дифференциал. Тормозные барабаны в двойном дифференциале установлены не на полуосях, как в простом дифференциале, а жестко связаны с тормозными солнечными шестернями.
Когда тормоза отпущены и сопротивления на обеих гусеницах равны, двойной дифференциал работает точно так же, как простой: сателлиты не вращаются вокруг своих осей, а увлекают обе шестерни полуосей с одинаковой скоростью. Обороты полуосей равны оборотам коробки сателлитов, и танк движется прямолинейно.
Если полностью затянуть один из тормозов, например правый, тормозная шестерня остановится. Как и при остановке шестерни полуоси в простом дифференциале, сателлит начнет вращаться вокруг своей оси, ускоряя вращение левой тормозной шестерни. Вместе с тормозным сателлитом начнет вращаться ведущий сателлит, посаженный с ним на одну ось. Ведущий сателлит находится в зацеплении с шестернями полуосей. Вращаясь, он замедляет вращение отстающей полуоси к ускоряет вращение забегающей: танк поворачивается.
Тот радиус, на котором танк поворачивается при полностью затянутом тормозе, будет расчетным, так как он наименьший; при этом радиусе мощность в тормозах не расходуется. У танка с простым дифференциалом отстающая гусеница при полностью затянутом тормозе останавливалась и расчетный радиус равнялся ширине колеи В, При двойном дифференциале расчетный радиус всегда больше ширины колеи, т. е.
Rр > В
В существующих конструкциях двойных дифференциалов расчетный радиус находится в пределах от 2В до 5В.
Так как расчетный радиус — наименьший, танк с двойным дифференциалом не может поворачиваться вокруг неподвижной гусеницы, как это возможно при простом дифференциале или бортовых фрикционах, поэтому поворотливость танка ухудшается. Можно подобрать шестерни двойного дифференциала так, что расчетный радиус будет равен В, как у простого дифференциала. Но тогда двойной дифференциал станет работать, как простой, и потеряет все преимущества, которые он имеет по сравнению с ним.
При повороте танка с двойным дифференциалом на расчетном радиусе вся мощность двигателя идет на преодоление внешних сопротивлений, как у всякого механизма поворота. Поворот с радиусом больше расчетного сопровождается пробуксовкой тормоза; при этом скорость забегающей гусеницы увеличивается, а отстающей уменьшается, хотя и не на столько, как при полной затяжке тормоза.
На рис. 508 показано распределение мощности при повороте с радиусом R=10В, когда расчетный радиус Rр= 5 В. Поскольку тормозана полуоси нет, мощность с отстающей гусеницы может возвращаться на забегающую гусеницу, т. е. в этом механизме происходит циркуляция мощности. В связи с этим уменьшаются потери мощности в тормозе; в нашем примере они составляют 3%, поэтому из 100% мощности, которая подводится на забегающую гусеницу, только 69% рщет от двигателя, а 31 % — от отстающей гусеницы.
4% мощности поступает к тормозу непосредственно от двигателя (сравните простой дифференциал, рис. 503), так что всего в тормозе затрачивается 7% мощности, т. е. несколько больше, чем у бортовой коробки или планетарного механизма с тем же расчетным радиусом. Но все же на этом радиусе поворота (10В) потеря мощности в тормозе в 5 раз меньше, чем у бортового фрикциона, и почти в 20 раз меньше, чем у простого дифференциала. При меньших расчетных радиусах выигрыш в мощности меньше, но даже при Rр=2В двойной дифференциал расходует в 4—5 раз меньше мощности в тормозах, чем простой, и примерно вдвое меньше, чем бортовой фрикцион.
Недостаток двойного дифференциала — ограниченная поворотливость танка вследствие большого расчетного радиуса (больше В).
Кроме того, двойному дифференциалу, как и всем вообще дифференциальным механизмам, присущ другой серьезный недостаток. Если сопротивление движению одной из гусениц станет больше, чем другой, например, если одна из гусениц погрузится в грязь или снег или если танк движется с креном на борт, танк будет «уводить» в сторону; как и при торможении одной полуоси, сателлиты начнут вращаться вокруг своих осей, ускоряя движение той гусеницы, на которой сопротивление меньше. При движении придется постоянно выравнивать танк тормозом, что усилит износ тормоза.
Если одна из гусениц буксует или сорвана, танк с дифференциалом перестает двигаться.
Выше указывалось, что скорость вращения полуосей танков с дифференциальными механизмами одинакова лишь в случае одинакового сопротивления на полуосях. Сопротивление движению танка под буксующей гусеницей значительно меньше, чем под той гусеиицей, где буксования нет, поэтому небуксующая гусеница останется неподвижной, а буксующая гусеница будет вращаться с удвоенной скоростью. Чтобы сдвинуть танк с места, надо затянуть тормоз буксующей гусеницы,
ПРИВОДЫ УПРАВЛЕНИЯ МЕХАНИЗМАМИ ПОВОРОТА
ТРЕБОВАНИЯ К ПРИВОДАМ УПРАВЛЕНИЯ МЕХАНИЗМАМИ ПОВОРОТА
Приводы управления механизмами поворота должны позволять механику-водителю поворачивать танк с любым радиусом — от наибольшего, когда танк движется прямолинейно, до наименьшего расчетного; при этом переход от одного радиуса к другому должен совершаться плавно.
Изменение радиуса поворота достигается сначала переключением передачи коробки (ступени механизма) отстающей гусеницы с высшей на низшую или с низшей на нейтраль, а затем регулированием пробуксовки тормоза или фрикциона.
Так, для получения различных радиусов поворота танка с двухступенчатым планетарным механизмом надо сначала выключить на отстающей стороне высшую (вторую) ступень и постепенно затягивать тормоз первой ступени до отказа, а потом выключить первую ступень и, перейдя на нейтраль, т. е. отъединив ведущее колесо отстающей гусеницы от двигателя, снова постепенно затягивать остановочный тормоз до отказа. Это правило действительно для любого независимого механизма. На танках с дифференциалом тормоз затягивается без отключения полуоси.
Таким образом, управление механизмами поворота сводится к чередованию включения и выключения фрикционных устройств в строгой последовательности. Управление правой и левой гусеницами осуществляется обычно отдельными рычагами, причем изменение положения рычага от крайнего переднего до крайнего заднего изменяет радиус поворота от наибольшего до наименьшего.
Значительно реже применяется для управления рулевое колесо (штурвал). Поворот штурвала вправо соответствует передвижению правого рычага, а поворот влево — левого.
Для торможения танка желательно иметь ножной привод, который воздействовал бы на оба остановочных тормоза, не влияя на механизмы поворота. Это особенно важно при спуске танка с горы.
Механизм управления должен быть устроен так, чтобы механик-водитель прилагал силу только на ту операцию, которая необходима в данный момент. Поясним это примером. Для поворота танка с бортовыми фрикционами нужно выключить один фрикцион, а затем затянуть тормоз. Допустим, что для выключения фрикциона требуется сила на рычаге, равная 20 кг, а для затяжки тормоза — 30 кг. При правильно устроенном механизме силу 20 кг механик-водитель прикладывает только до тех пор, пока фрикцион не выключится; в это время не требуется сила для затяжки тормоза. Когда фрикцион будет выключен, удерживать его пружины в сжатом положении механику-водителю не потребуется, так что на время затяжки тормоза ему придется приложить на рычаге силу только 30 кг.
ПРИВОД К ТОРМОЗУ
Простейший привод управления — привод к тормозу показан на рис, 512.

Рис. 512 Простейший привод к тормозу
Если передвигать рычаг, то вместе с ним будет передвигаться тяга, вызывающая затягивание тормоза; чем больше ход рычага, тем сильнее затягивается тормоз и тем меньше радиус поворота танка. При крайнем заднем положении рычага тормоз затянут до отказа, тормозной барабан не вращается, и танк поворачивается с расчетным радиусом. Такое устройство позволяет выполнять только одну операцию — затягивать тормоз; следовательно, оно пригодно лишь для управления дифференциалами — простым или двойным.
ПРИВОД УПРАВЛЕНИЯ БОРТОВЫМ ФРИКЦИОНОМ И ТОРМОЗОМ
На рис. 513 показан привод управления бортовым фрикционом и тормозом.

Рис. 513 Привод управления бортовым фрикционом и тормозом
Сравнительно с рассмотренным ранее этот привод сложнее. Он состоит из двух тяг, одна из которых разрезная. Половины разрезной тяги соединены вилкой с прорезью, в которую входит палец. В начале хода рычага управления тормоз не затягивается. Передняя половина тормозной тяги движется, а палец свободно скользит в прорези вилки задней половины тяги до тех пор, пока не упрется в конец вилки. Лишь после этого тормоз начинает затягиваться.
Таким образом, в начале хода рычага происходит выключение фрикциона, после чего начинается затяжка тормоза. Тяга фрикциона в таком приводе движется все время, пока перемещается рычаг управления, даже после того, как фрикцион выключится; поэтому во время торможения работа механика-водителя бесполезно затрачивается на дополнительное сжатие пружин фрикциона. Такой привод хотя и обеспечивает надлежащую последовательность операций управления, но не разделяет сил. Его применяли только на легких танках, для управления которыми не требовалось значительной силы.
РАЗДЕЛИТЕЛЬ
Чтобы уменьшить силу, необходимую для управления механизмами поворота, в привод вводят разделитель (рис. 514).
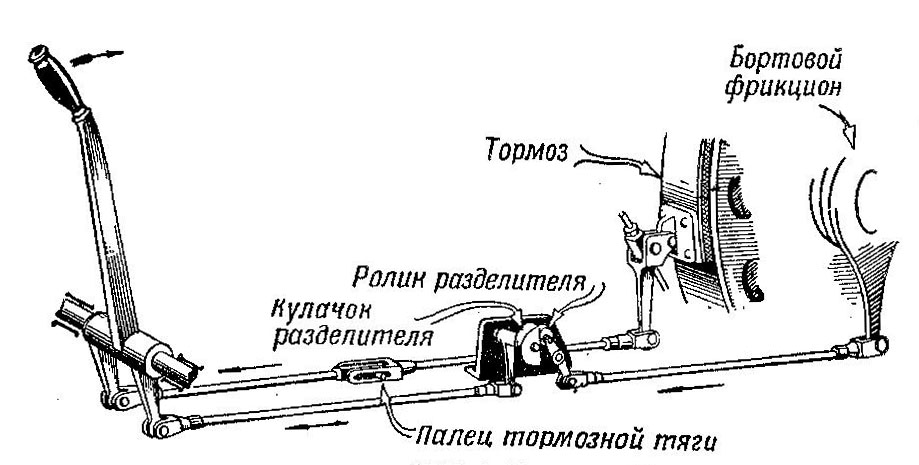
Рис. 514 Привод с разделителем
Для этого конец передней тяги, идущей от рычага управления, соединяют с валиком, на котором сидит кулачок разделителя. Кулачок разделителя (рис. 514, 515, А) представляет собой шайбу, имеющую рабочую и нерабочую поверхности (профили).
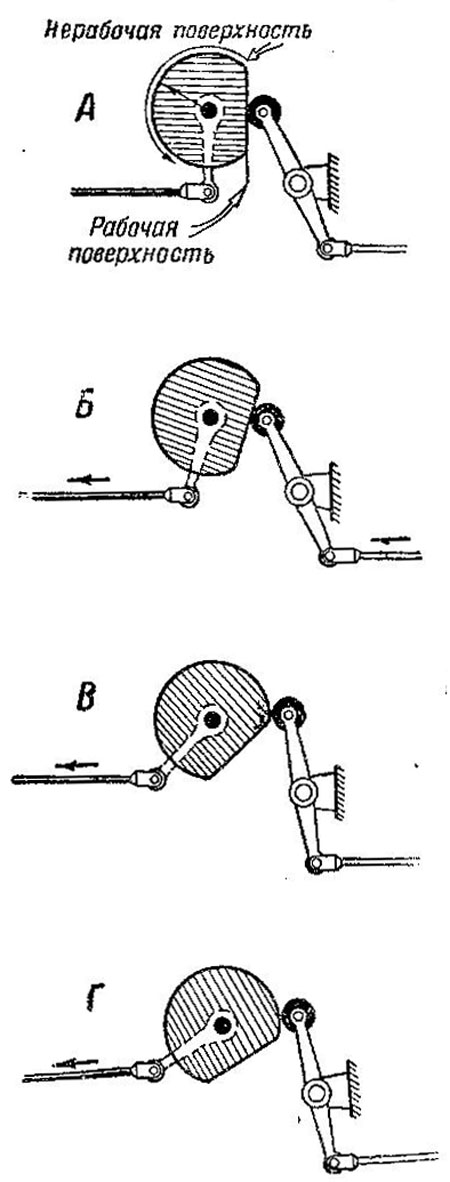
Рис. 515 Работа разделителя
Форма рабочего профиля, такая, что, когда кулачок поворачивается, ролик, прижатый к нему, отходит назад. При этом тяга, идущая к фрикциону, перемещается, выключая фрикцион (рис. 515, Б). Второй профиль — нерабочий — представляет собой дугу окружности, центр которой находится на оси кулачка. Катясь по этойокружности, ролик не перемещается. Следовательно, не происходит и дальнейшего сжатия пружин фрикциона (рис, 515,В и Г), Пока происходит выключение фрикциона, тормоз еще не затягивается, так кай палец рычажка тормоза скользит в.прорези вилки тяги (см, рис. 514). Когда фрикцион выключится полностью, палец тормозной тяги пройдет всю прорезь, упрется в переднюю стенку вилки, и тормоз начнет затягиваться.
Во время выключения фрикциона, пока ролик катится по рабочему профилю ку лачка, сжатые пружины фрикциона, стремясь разжаться, действуют через детали меха-низма выключения и привода и прижимают ролик к кулачку (рис. 516, вверху).

Рис. 516 Силы, действующие на кулачок разделителя
Таким образом, со стороны ролика на кулачок действует сила, стремящаяся сдвинуть кулачок. Линия действия этой силы не проходит через ось кулачка, поэтому она вместе с вызываемой ею силой сопротивления, приложенной к оси кулачка, создает пару сил. Эта пара сил препятствует повороту кулачка все то время, пока ролик катится по рабочему профилю. Чтобы повернуть кулачок, механик-водитель должен приложить силу к рычагу управления. Когда ролик перейдет на нерабочий профиль (рис. 516, внизу), линия действия силы от сжатых пружин проходит через ось кулачка, и плечо пары сил равно нулю. Следовательно, механику-водителю после выключения фрикциона приходится прилагать силу к рычагу лишь для затяжки тормоза, в дополнение к этому требуется небольшая сила для преодоления трения ролика, катящегося по кулачку,
ПРИВОД УПРАВЛЕНИЯ МНОГОСТУПЕНЧАТЫМИ МЕХАНИЗМАМИ
Если механизм поворота имеет не одну, а несколько ступеней (несколько расчетных радиусов), привод управления будет более сложным, так как в таком механизме больше тормозов или фрикционов, которые должны при различных положениях рычага управления вступать в работу и прекращать ее.
Для примера рассмотрим принципиальную схему привода управления двухступенчатым планетарным механизмом поворота (рис. 517).
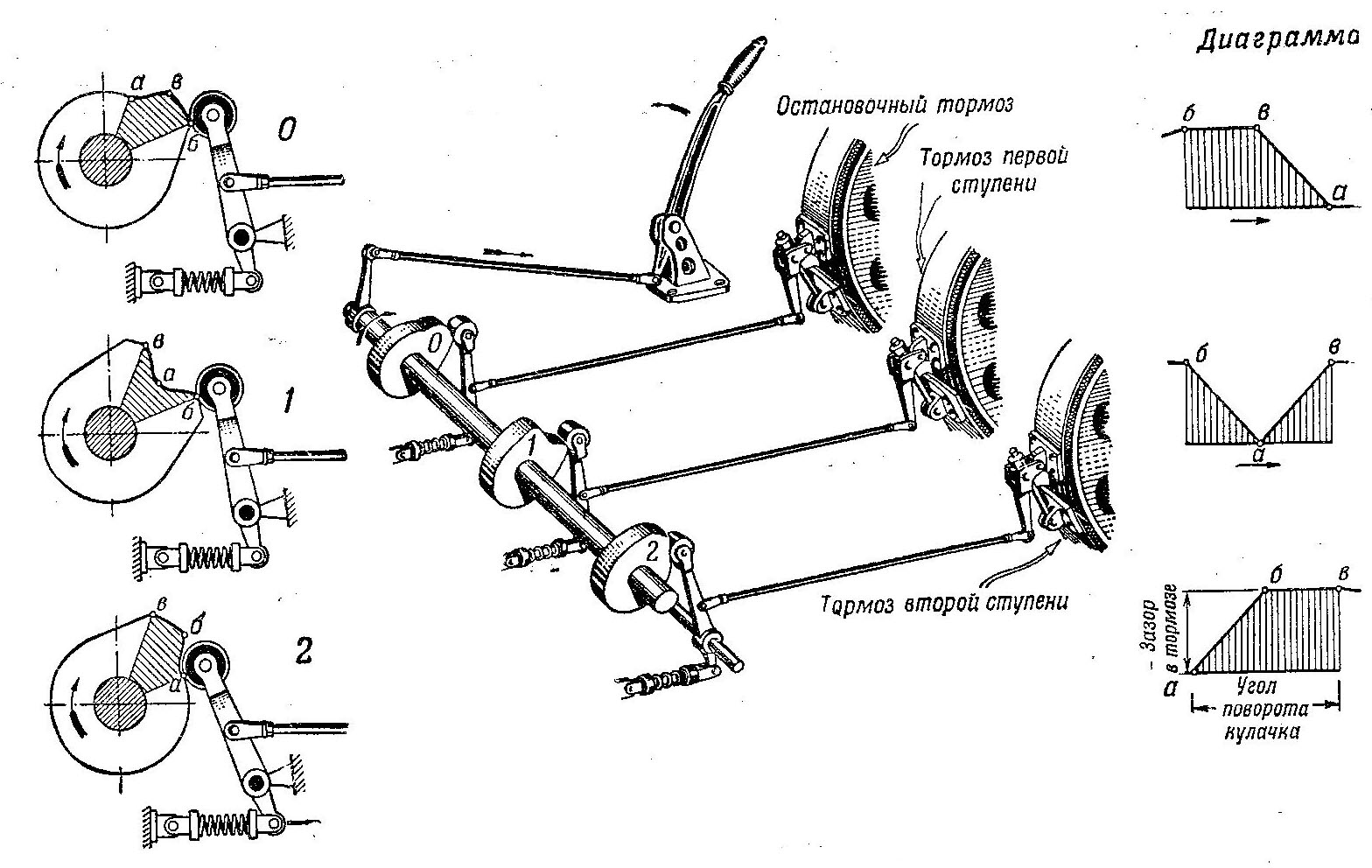
Рис. 517 Работа привода управления двухступенчатым механизмом поворота танка
В этом механизме два тормоза планетарных передач и один остановочный тормоз. Один из тормозов планетарных передач может быть заменен фрикционом, работа привода при этом не изменится. Для управления тремя тормозами служит валик с тремя различными по форме кулачками. Каждый из кулачков при повороте валика действует на ролик, связанный тягой с одним из тормозов. Ролик всегда прижат пружиной к кулачку. Пружины стремятся разжаться и тем самым затянуть тормоз.
Когда рычаг управления находится в крайнем переднем положении, в механизме включена вторая передача (ступень). Тормоз этой передачи затянут до отказа и удерживается в этом положении пружиной,. остальные два тормоза отпущены. Ролик 2 этой передачи (рис. 517, внизу) входит в выемку кулачка у точки а, но не касается его, так как тормоз полностью затянут (зазор между лентой и барабаном равен нулю, см. диаграмму справа). Легко понять, что, если бы ролик касался кулачка,. полной затяжки не было бы. Другие два ролика (1 и 0на рис. 517) касаются своих кулачков в точках б. Значки не дают пружинам переместить тяги и затянуть тормоза; оба тормоза отпущены (по диаграмме зазор между лентой и барабаном наибольший). Сила сжатых пружин не передается рычагу управления, так как линия действия сил проходит через ось валика, на котором сидит кулачок, как в рассмотренном выше случае с разделителем.
При движении рычага управления по стрелке валик поворачивается. Кулачок 2, действуя на ролик, двигает тягу, отводя ролик и отпуская тормоз. Вторая ступень выключается, и зазор в тормозе увеличивается (см. диаграмму). Одновременно кулачок 1освобождает ролик первой ступени, и тормоз этой ступени под действием пружины затягивается; зазор между лентой и барабаном тормоза постепенно уменьшается до нуля. Ролик 0остановочного тормоза катится по нерабочему профилю кулачка, так что остановочный тормоз не затягивается, и зазор в нем остается прежним (участок б-в верхней диаграммы).
Так продолжается, пока ролик 2 не дойдет до точки б, ролик 1 — до точки а и ролик 0 — до точки в. В тот момент, когда ролики 2, 1 и 0достигнут указанных точек, первая ступень полностью включится.
При дальнейшем движении рычага ролик 2 катится по нерабочей поверхности б-в кулачка, и зазор в тормозе второй ступени остается постоянным (участок б-в нижней диаграммы). Кулачок 1, нажимая на ролик (участок а-в средней диаграммы), выключает тормоз первой ступени, зазор в тормозе увеличивается, и первая ступень выключается. В то же время кулачок 0освобождает ролик, катящийся по участку в-а, и пружина затягивает остановочный тормоз. Движение рычага управления в обратном направлении приводит тормоза в действие в обратном порядке.
Сравнивая рассмотренный нами привод управления с приводами для более простых механизмов, нетрудно убедиться, что последние представляют собой более или менее сложные варианты основной схемы. Для одноступенчатого механизма (бортовой фрикцион с тормозом) достаточно двух кулачков (вместо трех), а для упрощения устройства один кулачок можно заменить прорезью в видке тормозной тяги (см. рис. 514).
Если отказаться от разделения сил, например на легком танке, кулачки могут быть заменены двумя тягами, из которых одна будет с прорезью (см. рис. 513) или двумя рычагами разной длины (рис. 518).
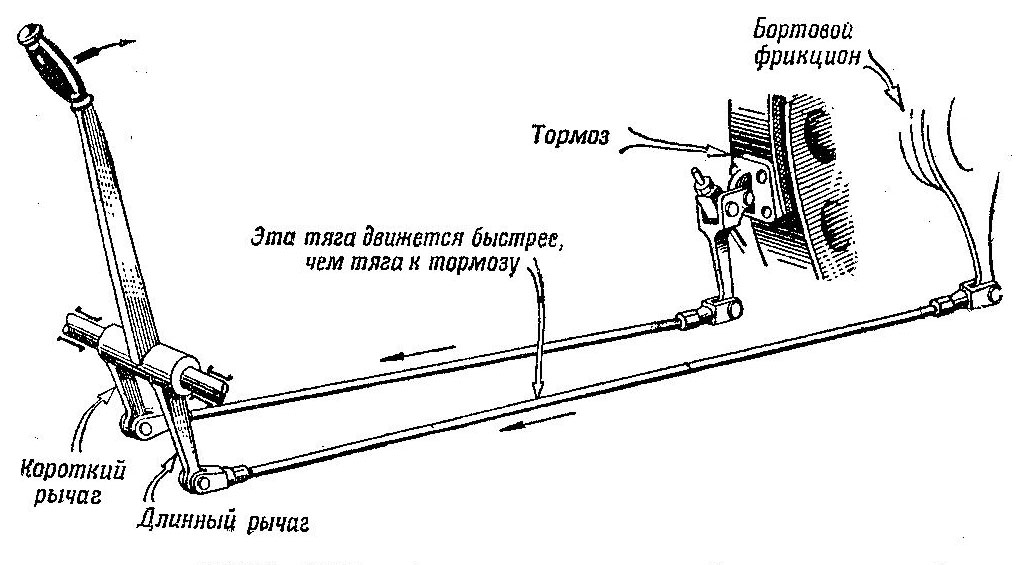
Рис. 518 На легких танках иногда применялся простой привод, имеющий дварычага разной длины
Короткий рычаг связан тягой с тормозом, длинный — с бортовым фрикционом. Так как тяга длинного рычага перемещается быстро, фрикцион выключится раньше, чем затянется тормоз.
Наконец, для дифференциала требуется всего один кулачок, поэтому рычаг управления можно соединить тягой непосредственно с тормозом так же, как это было показано на рис. 512.
Для управления механизмами поворота применяют сервоустройства, подобные рассмотренным выше устройствам для выключения главного фрикциона и переключения передач. В этом случае рычат управления механизмами поворота воздействует на клапаны (краны) , через которые сжатый воздух или жидкость проходит в рабочие цилиндры. Когда какой-нибудь цилиндр включается, соответствующий тормоз затягивается (или фрикцион выключается), когда тот же цилиндр выключается — тормоз отпускается.
РЕГУЛИРОВКА ПРИВОДОВ
Приводы управления регулируются с целью обеспечитъ нужную последовательность, а также своевременное начало и конец работы каждого из тормозов илифрикционов. Это достигается установкой роликов и ку-лачков (пальцев в прорезях тяг) в строго определенном взаимном положении друг к другу.
Фрикционные механизмы необходимо заранее отрегулировать. Фрик-ционы надо отрегулировать на полное включение и выключение; в тормозах должен быть отретулирован нормальный зазор между лентой (колодкой, если тормоз колодочный) и барабаном.
Неправильная регулировка механизмов и приводов управления приводит к нарушению работы механизмов поворота, (вследствие чего танк поворачивается плохо или совсемне поворачивается. Так, если остановочный тормоз затягивается слишком рано, он тормозит отстающую гусеницу, не отключенную от двигателя, т. е. к тормозу подводится мощность двигателя. Двигатель при этом может заглохнуть, а тормоз прийти в негодность от чрезмерного нагрева. Если эазор в тормозе слишком велик, соответствующая передача (ступень) механизма поворота не включается полностью, танк не поворячивается с расчетнымм радиусом, а тормоз все время буксует и перегревается.
ТРАНСМИССИИ С ДВОЙНЫМ ПОДВОДОМ МОЩНОСТИ
В рассмотренных выше трансмиссиях механизмы поворота работают независимо от других механизмов трансмиссии в том смысле, что устройство последних ни в какой мере не влияет на радиусы поворота танка и на расход мощности в тормозах. В частности, замена в трансмиссии одной коробки передач другой, с другим числом передач и другими передаточными числами, непосредственно не отразится на (поворотливости танка; его влияние скажется лишь косвенно, поскольку силы тяги и скорости движения танка изменятся.
При обычном разделении трансмиссии на два самостоятельных узла. — коробку передач для прямолинейного движения, механизмы поворота для осуществления поворота — автоматической связи между скоростью танка и радиусом его поворота не будет.
Однако в некоторых трансмиссиях такая связь существует: при большой скорости движения поворот совершается только с большими радиусами, при малых — с любыми, не исключая и самых малых, необходимых для обеспечения достаточной маневренности танка.
Трансмиссии такого типа называются трансмиссиями с двойным подводом мощностьтак как мощность к механизмам поворота подводится в них двумя потоками. В таких трансмиссиях механизмы поворота и коробка передач работают как одно целое. Существен ной особенностью этих трансмиссий является наличие различных радиусов поворота на каждой передаче вкоробке передач. Таких радиусов обычно бывает один, реже два, поэтому общее число расчетных радиусов поворота танка равно обычно числу передач коробки, т. е. не менее четырех. Высшим передачам (большим скоростям) соответствуют большие радиусы поворота, низшим—малые.
Трансмиссии подобного типа могут различаться по устройству, но все они объединены одной общей чертой: их механизмы поворота имеют двойную связь с двигателем — через коробку передач и помимо нее; поэтому такие трансмиссии несколько сложнее рассмотренных нами обычных трансмиссий, что является их недостатком.
Остановимся на схемам двух трансмиссий с двойным подводом мощности —дифференциальной и независимой.
ТРАНСМИССИЯ С ДИФФЕРЕНЦИАЛОМ
На рис. 519 приведена принципиальная схема трансмиссии с дифференциалом, а на рис. 520 — схема ее устройства.
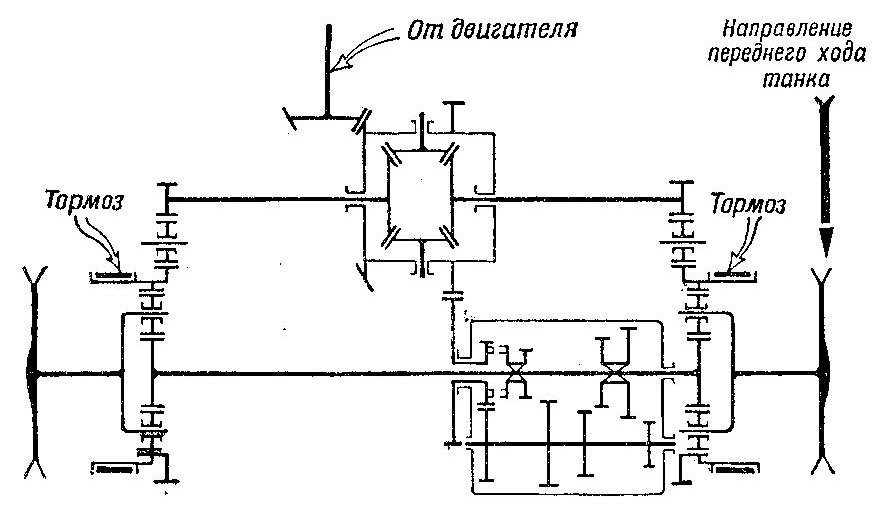
Рис. 519 Принципиальная схема дифференциальной трансмиссии с двойнымподводом мощности
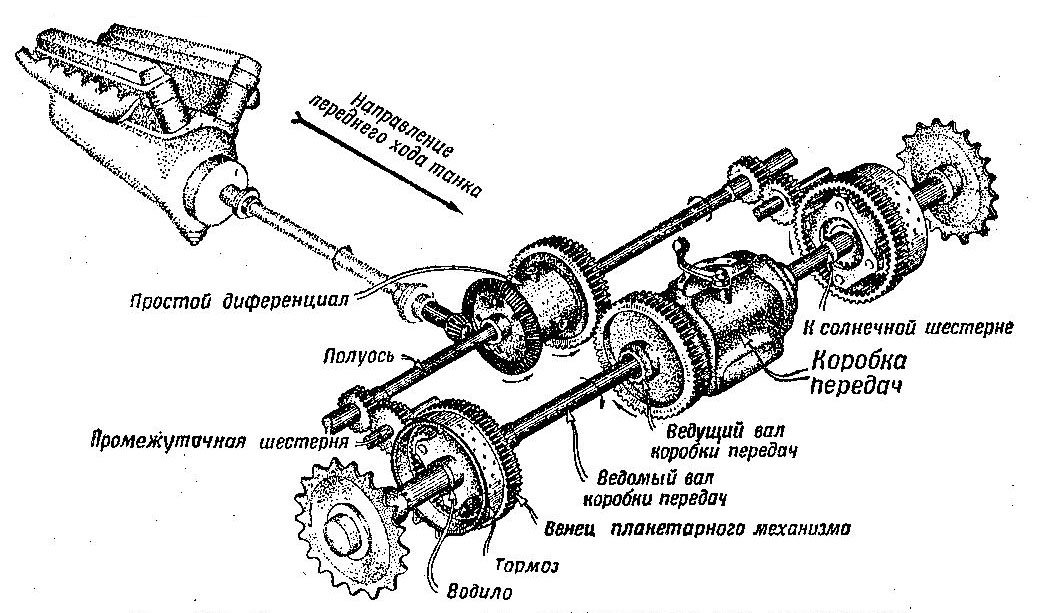
Рис. 520 Конструктивная схема дифференциальной трансмиссия
Коленчатый вал двигателя через карданный вал и коническую передачу приводит во вращение коробку сателлитов простого дифференциала. От коробки сателлитов вращение передается через пару шестерен полому ведущему валу коробки передач. Внутри ведущего вала проходит ведомый вал коробки передач. На обоих концах ведомого вала установлены солнечные шестерни планетарных передач. Зубчатые венцы планетарных передач приводятся во вращение полуосями дифференциала через промежуточные (паразитные) шестерни. Кроме того, венцы могут тормозиться установленными на них тормозами.
В планетарных передачах, рассмотренных нами выше, одна из деталей — солнечная шестерня или венец — в рабочем положении была неподвижна. В данном механизме врабочем положении вращаются и солнечная шестерня и венец. Из рис. 519 и 520 видно, что они вращаются в разные стороны. Сателлиты в этом случае вынуждены двигаться вокруг солнечной шестерени приводить во вращение водило. Но водило делает меньше оборотов, чем при неподвижном венце. В этом легко убедиться, если рассмотреть пример с рычажками, заменяющими сателлиты (рис.521).
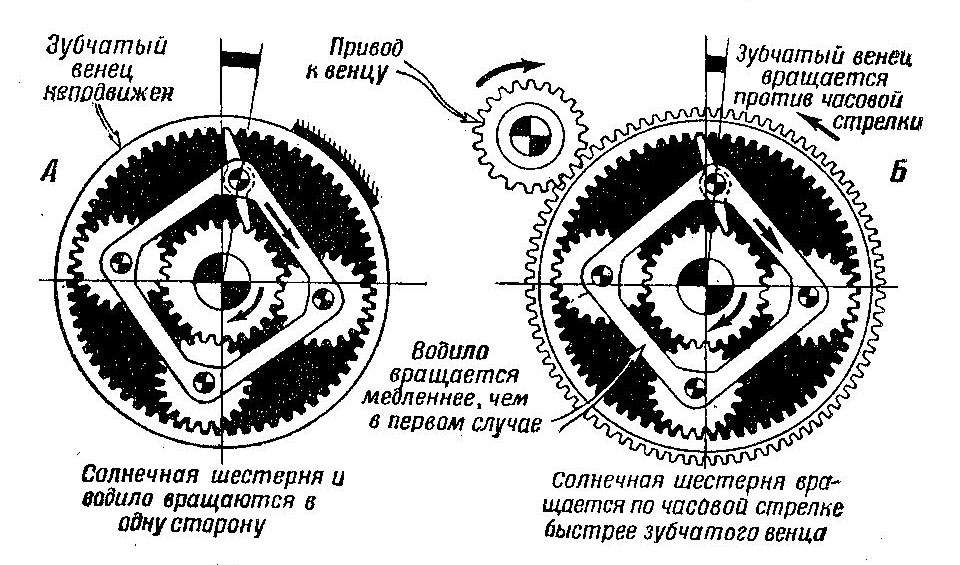
Рис. 521 Работа планетарного механизма при неподвижном и вращающемся венце
Так как один конец рычажка, связанный с венцом перемещается в одну сторону, а другой, связанный с солнечной шестерней (рис. 521,Б),—в другую, середина рычажка (водило) будет двигаться медленнее, чем в том случае, когда один конец неподвижен (рис. 521, А). Направление движения середины рычажка, т. е. направле-ние вращения водила, определяется числом оборотов солнечной шестерни и венца, точнее — соотношением их окружных скоростей. В рассматриваемой нами схеме солнечная шестерня вращается значительно быстрее венца. Следовательно, водило будет вращаться в ту же сторону, что и солнечная шестерня.
Предположим, что тормоза венцов отпущены. Числа оборотов солнечных шестерен одинаковы, так как обе ониустановлены на ведомом валу коробки передац. Числа оборотов обоих венцов также одинаковы, поскольку равны числа оборотов полуосей дифференциала (дифференциал вращается как одно целое), поэтому оба водила также имеют одинаковые обороты и танк движется прямолинейно.
Затянем до отказа тормоз одного из венцов, например левого. Венец остановится, а число оборотов оолнечной шестерни останется прежним, поэтому число оборотов левого водила увеличится и, поскольку водило связано с ведущим колесом, скорость левой гусеницы возрастет. Вследствие торможения левого венца остановится левая полуось дифференциала, число оборотов правой полуоси удвоится, и правый венец начнет вращаться вдвое быстрее, чем при прямолинейном движении. Так как он вращается в противоположном направлении по отношению к солнечной шестерне (притормаживает водило), то правое водило уменьшит число оборотов, и скорость правой гусеницы снизится.
Таким образом, при затяжке левого тормоза танк будет поворачи ваться направо, а при затяжке правого— налево. Разумеется, для сохранения привычного управления танком левый рычаг должен обеспечивать левый поворот, а правый рычаг — правый, ввиду этого левый рычаг соединяют с правым тормозом и, наоборот, правый рычаг — с левым тормозом.
Каким же образом на каждой передаче получается свой расчетныйрадиус поворота?
Пусть танк движется на третьей передаче и солнечные шестерни обоих планетарных рядов делают по 3000 об/мин, а венцы, вращающиеся в обратную сторону, по 200 об/мин. При этом размеры шестерен планетарных передач таковы, что каждое водило, вращаясь в ту же сторону, что и солнечная шестерня, делает 1100 об/мин.
Затормозим до отказа левый венец. Левое водило вследствие этого начнет вращаться быстрее и будет делать 1200 об/мин. Обороты правого венца, связанного с левым через дифференциал, увеличатся вдвое, т. е. до 400 об/мин, поэтому число оборотов правого водила упадет до 1000 об/мин. Танк повернется вправо, причем данному соотношению ско ростей гусениц соответствует расчетный радиус поворота 6В.
Положим далее, что на первой передаче солнечные шествии делают 1200 об/мин. Так как венцы связаны с двигателем помимо коробки передач, то их обороты попрежнему равны 200 об/мин. Водила в этом случае делают около 350 об/мин. При торможении левого венца обороты левого водила возрастут почти до 500 об/мин, а обороты правого уменьшатся до 250 об/мин. При таком соотношении скоростей гусениц радиус поворота равен 2В.
Таким образом, благодаря двойной связи планетарной передачи с двигателем — через коробку передач и помимо нее — отношения скоростей забегающей и отстающей гусениц, а следовательно, и расчетные радиусы поворота на разных передачах будут различны. Чем выше передача, тем больше радиус поворота и наоборот. Так, на третьей передаче при остановке венца обороты одного водила увеличиваются, а другого уменьшаются всего на 10%, вто время как на первой передаче ввиду меньшей скорости солнечной шестерни изменение оборотов достигает 30%.
Таким же точно образом работает передача, если с ведомым валом коробки соединен венец, а с полуосями дифференциала — солнечные шестерни.
Итак, количество расчетных радиусов соответствует числу передач коробки. Кроме того, при такой трансмиссии возможен поворот танка с Rр=B и Rр=B/2 Нетрудно убедиться, что трансмиссия работает с циркуляцией мощности.
Управление поворотом сводится к затяжке тормоза, как при простом дифференциале.
ТРАНСМИССИЯ БЕЗ ДИФФЕРЕНЦИАЛА (НЕЗАВИСИМАЯ)
Схема независимой трансмиссии (без дифференциала) показана на рис. 522.
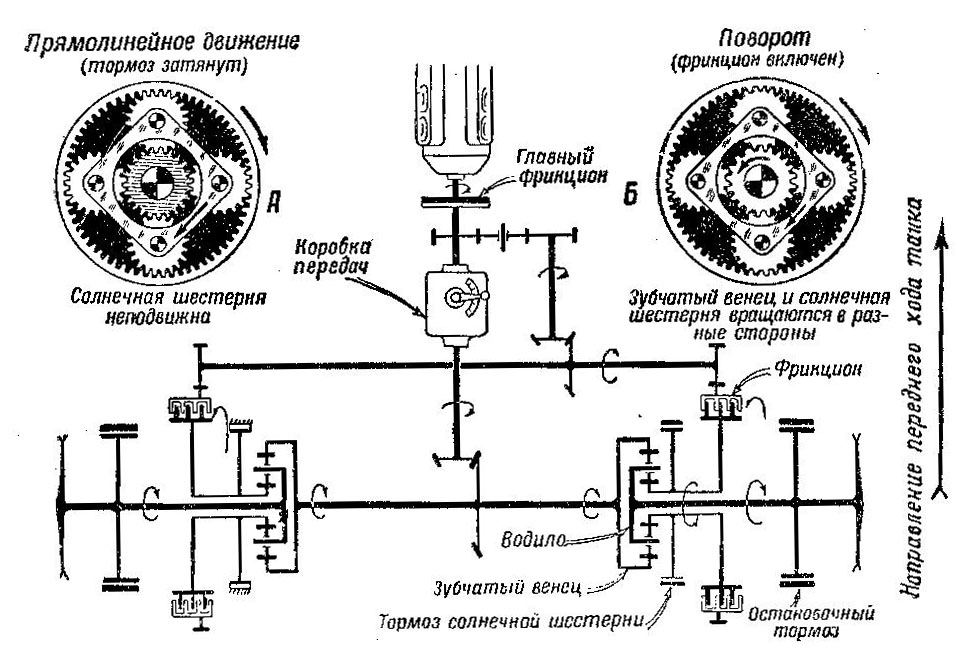
Рис. 522 Схема независимой трансмиссии с двойным подводом мощности
В ней дифференциал заменен двумя фрикционами. Ведущий барабан каждого фрикциона соединен с коленчатым валом двигателя при помощи цилиндрических и конических шестерен, помимо коробки передач. Ведомый барабан фрикциона связан с солнечной шестерней планетарного механизма, на валу которой, кроме того, установлен тормоз.
Когда танк движется прямолинейно, оба тормоза солнечных шестерен затянуты, а фрикционы выключены. Солнечные шестерни не вращаются (положение А). Двигатель через коробку передач и нижний поперечный вал вращает зубчатые венцы. Сателлиты, обкатываясь вокруг солнечных шестерен, увлекают за собой водила и связанные с ними ведущие колеса танка.
Чтобы повернуть танк, надо отпустить тормоз солнечной шестерни и включить фрикцион (положение Б). Солнечная шестерня начнет вращаться в сторону, противоположную направлению вращения зубчатого венца.
Так как венец увлекает водило в одну сторону, а солнечная шестерня старается увлечь его в другую, число оборотов водила и соединенной с ним гусеницы уменьшается, поэтому танк поворачивается в сторону включенного фрикциона.
Расчетный радиус поворота определяется соотношением чисел обо ротов венца и солнечной шестерни. Обороты солнечной шестерни не зависят от передачи, включенной в коробке, так как фрикцион соединяет солнечную шестерню с двигателем, минуя коробку, а число оборотов венца тем меньше, чем ниже передача; поэтому расчетные радиусы на разных передачах будут различными, как и в предыдущем случае.
В отличие от рассмотренного выше дифференциального механизма, данный механизм не увеличивает скорости забегающей гусеницы при повороте, так как число оборотов ее венца остается прежним, а солнечная шестерня не вращается. В этом заключается одно из преимуществ данной трансмиссии по сравнению с дифференциальной. Другим преимуществом только что рассмотренной трансмиссии является то, что при помощи фрикционов можно увеличивать силу тяги на ведущих колесах, не переходя на низшую передачу. Если на обоих бортах отпустить тормоза и включить фрикционы, число оборотов ведущих колес уменьшится, а сила тяги возрастет. Это значит, что рассмотренным планетарным механизмом можно пользоваться как демультипликатором; в этом отношении он схож с двухступенчатым планетарным механизмом поворота.
При прямолинейном движении танка с включенными фрикционами поворот производится путем выключения одного фрикциона и затяжки остановочного тормоза, как при обычном бортовом фрикционе. Расчетный радиус поворота в этом случае всегда будет равен ширине колеи.
Выясним, какой величины должны быть расчетные радиусы, чтобы танк имел возможность поворачиваться на всех передачах.
Пусть расчетные скорости танка на передачах известны. Тогда можно, пользуясь данными графика на рис, 489, определить мощность внешних сопротивлений для всех радиусов. На рис. 523 приведены подсчитанные таким путем мощности для трансмиссии без дифференциала.
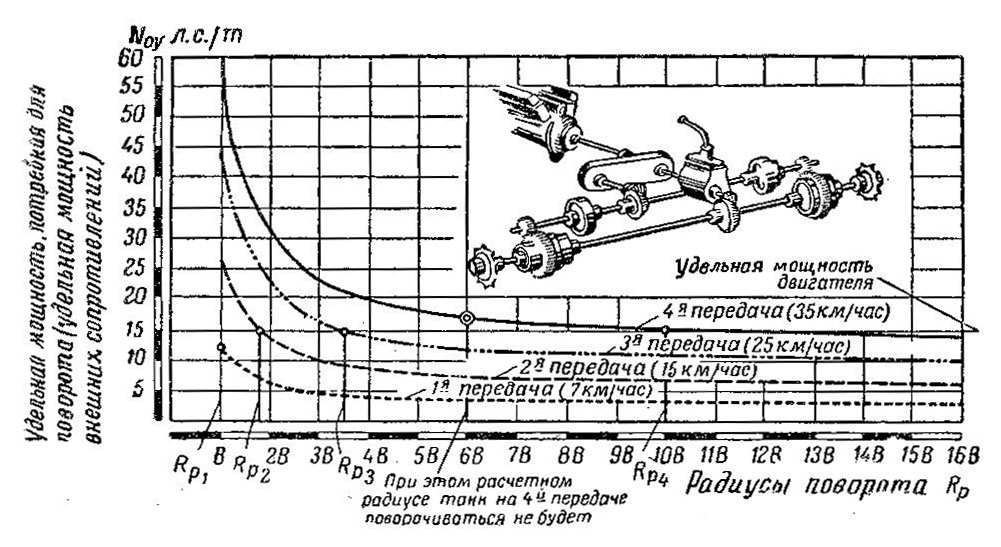
Рис. 523 Зависимость удельной мощности внешних сопротивлений от радиуса допорота и скорости на передачах в трансмиссии без дифференциала
Понятно, что чем выше передача (больше скорость), тем больше и мощность внешних сопротивлений.
График позволяет определить расчетные радиусы для каждой из передач. Действительно, мощность внешних сопротивлений не должна превышать мощность двигателя, иначе поворот будет невозможен. Пусть удельная мощность двигателя равна 15 л.с./т. Тогда пересечение горизонтальной линии, соответствующей 15 л.с/т, с кривыми графика определит наименьшую величину расчетного радиуса для данной передачи. Так, на четвертой передаче расчетный радиус должен быть не менее 10В. Если принять его равным 6В (см, рис. 523), танк на этом радиусе с данной скоростью повернуться не сможет, так как не хватит мощности двигателя.
На рис. 524 приведен подобный же график для трансмиссии с дифференциалом.

Рис. 524 Зависимость мощности внешних сопротивлений от радиуса поворота и скорости на передачах в трансмиссии с дифференциалом
Увеличение мощности в этом случае объясняется тем, что скорость забегающей гусеницы при повороте будет больше, чем она была при прямолинейном движении, Увеличение скорости забегающей гусеницы тем больше, чем меньше радиус поворота.
Совершенно естественно, что расчетные радиусы для дифференциальной трансмиссии получаются большими, чем для трансмиссии без дифференциала.
ПОВОРОТ ТАНКА С ГИДРАВЛИЧЕСКОЙ ТРАНСМИССИЕЙ
При гидравлической трансмиссии на танке могут быть установлены механизмы поворота любого типа — фрикционы, планетарные, дифференциалы и т. д. В этом случае поворот не будет отличаться от поворота танка с обычной коробкой передач.
Если установить в трансмиссии планетарные механизмы с двойным подводом мощности, т. е. соединить одну из шестерен планетарного ряда с коленчатым валом двигателя, минуя гидравлическую передачу, а другую— через гидравлическую передачу (на рис. 519 и 522 гидравлическая передача займет место коробки передач), то поворот на любом радиусе может происходить без потери мощности в тормозах. Однако поворот будет неустойчивым даже при полностью затянутом тормозе (включенном фрикционе).
Действительно, пусть танк с гидравлической передачей, установленной по схеме рис. 522, движется прямолинейно. Скорость танка в этом случае, как было показано в предыдущей главе, устанавливается автоматически, в зависимости от сопротивления движению. Включим фрикцион отстающей гусеницы. Начнется поворот, и сопротивление на забегающей гусенице увеличится, что вызовет уменьшение числа оборотов ведомого вала гидравлической передачи, соединенного с венцами планетарных рядов. Произойдет как бы переход на низшую передачу. Но каждой «передаче» соответствует свойрадиус поворота. Поэтому непрерывно меняющиеся сопротивления вызовут непрерывное изменение радиуса поворота. При этом скорость забегающей гусеницы уменьшается по сравнению с прямолинейным движением и для поворота танка требуется меньшая мощность. Это выгодно, но так как радиус поворота установится самопроизвольно, то, чтобы танк повернулся с нужным радиусом, придется заставить фрикцион пробуксовывать. Следовательно, в действительности поворот без потери мощности в фрикционе (тормозе) на любом заданном радиусе невозможен и при гидравлической трансмиссии.
ПОВОРОТ ТАНКА С ЭЛЕКТРИЧЕСКОЙ ТРАНСМИССИЕЙ
Вотличие от танков с механической трансмиссией, в танках с электрической трансмиссией легко объединить механизмы, обеспечивающие изменение силы тяги и скорости при прямолинейном движении, с механизмами поворота, если установить два электромотора — по одному на каждую гусеницу.
Рассмотрим поворот танка с электрической трансмиссией, схема которой была дана в предыдущей главе. Схема работы трансмиссии при повороте показана на рис. 525.

Рис. 525 Схема работы электрической трансмиссиипри повороте танка
Чтобы повернуть танк, при помощи реостата увеличивают силу тока, идущего в обмотку возбуждения электромотора отстающей гусеницы. Как уже говорилось в предыдущей главе, увеличение тока в обмотке возбуждения вызывает снижение оборотов электромотора, а значит, и снижение оборотов, ведущего колеса отстающей гусеницы.
Забегающая; гусеница через корпус увлекает отстающую гусеницу, стремясь заставить ее вращаться быстрее, чем ее вращает электромотор. В этом случае электромотор перестает быть источником движения, и гусеница через ведущее колесо вращае его якорь Это значит, что электромотор становится генератором. Он уже не потребляет ток от основного генератора. Наоборот, сам электромотор М1отстающей гусеницы подает ток в общую цепь, передающу энергию электромотору М2 забегающей гусеницы. Тем самым облегчается работа основного генератора Г, а значит, и двигателя. Необходимо только, чтобы напряжение на щетках электромотора (ставшего генератором) было равно напряжению на щетках основного генератора; тогда в сети окажутся два источника тока, соединенных параллельно и питающих один и тот же потребитель — электромотор забегающей гусеницы.
При повороте танка с электрической трансмиссией происходит циркуляция мощности совершенно так же, как при повороте танка с двойным дифференциалом или планетарными механизмами, имеющими расчетный радиус больше В.
Существование циркуляции мощности доказывалось ранее только путем рассуждений. В данном же случае возвращаемая мощность может быть замерена приборами. Если в цепь включить амперметр, он покажет, что при повороте танка ток идет не к электромотору отстающей гусеницы, а от него — к электромотору забегающей гусеницы.
Радиус поворота определяется тормозной силой, создаваемой на отстающей гусенице, т. е. в конечном счете силой тока в обмотке возбуждения электромотора этой гусеницы. Устойчивость поворота танка с электрической трансмиссией не обеспечивается, так как изменение сопротивления автоматически вызывает изменение скоростей гусениц и радиусов поворота.
Надо заметить, что неустойчивым будет также и прямолинейное движение, поскольку изменение сопротивления движению одной из гусениц вызовет изменение числа оборотов ее электромотора и танк будет уводить в сторону (как при дифференциале).
Из сказанного следует, что при электрической трансмиссии поворот без потерь может происходить на всех радиусах, на которых напряжение электромотора отстающей гусеницы не ниже напряжения генератора. Если при каком-либо радиусе поворота последнее условие не соблюдено (например, когда сила тока возбуждения достаточно велика, но малы обороты якоря), поворот можно будет произвести при помощи реостата, включенного между генератором и электромотором (на схеме не показан); при этом мощность двигателя будет тратиться на нагрев реостата так же, как она тратится на нагрев тормозов в обычных трансмиссиях.
Все сказанное относится к радиусам поворота, величина которых больше ширины колеи. Чтобы произвести поворот с радиусом меньше ширины колеи, переключают ток (изменяют его направление) в обмотке возбуждения электромотора отстающей гусеницы. Так как направление вращения якоря изменится, гусеница начнет вращаться в обратную сторону.
На некоторых танках с электротрансмиссией поворот осуществлялся при помощи тормозов, как в обычных трансмиссиях; это позволяло более точно регулировать поворот, но в тормозах расходовалась часть мощности двигателя точно так же, как это происходит в других механизмах поворота.
СРАВНИТЕЛЬНАЯ ОЦЕНКА МЕХАНИЗМОВ ПОВОРОТА
Как мы уже указывали, поворотливость танка оценивается двумя величинами; угловой скоростью поворота и наименьшим радиусом, с которым может совершаться поворот. Чем выше угловая скорость, тем танк маневреннее, тем меньше времени потребуется на совершение поворота с одним и тем же радиусом.
Если подойти к оценке механизмов поворота с этой точки зрения, то надо отметить, что на одной и той же передаче коробки передач танк с дифференциалом будет иметь большую угловую скорость, чем танк с независимыми механизмами. Действительно, при повороте танка с дифференциалом скорость его забегающей гусеницы возрастет на столько, на сколько снизится скорость отстающей гусеницы v1(рис. 526), при этом средняя скорость достается такой же, какой она была при прямолинейном движении.
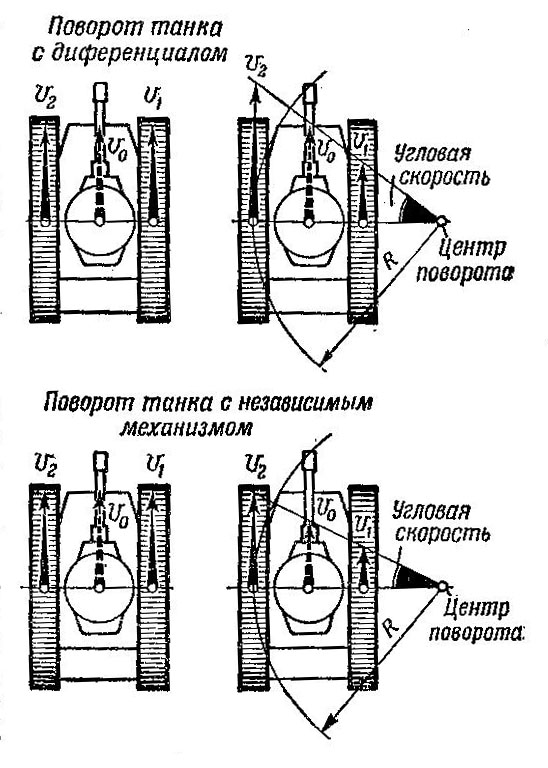
Рис. 526 Скорость танка при повороте с дифференциалом и независимыми механизмами
У танка с независимыми механизмами неизменной остается скорость забегающей гусеницы, если, конечно, не меняется число оборотов коленчатого вала двигателя. Но тогда при одном и том же радиусе поворота средняя скорость v0должна уменьшиться. Как видно из графика, угловая скорость танка с дифференциалом будет выше, чем скорость танка с независимыми механизмами.
Однако при повороте с более высокой средней скоростью увеличится потребная мощность двигателя. Если на данной передаче мощности не хватит, придется перейти на более низкую передачу, т. е. снизить угловую скорость поворота танка, поэтому обеспечение высокой угловой скорости поворота следует проверять по расходу мощности, затрачиваемой на поворот. Потребная мощность будет тем меньше, чем меньше мощности тратится в тормозах.
Величина расходуемой тормозной мощности позволяет одновременно оценить надежность фрикционных механизмов (фрикционов или тормозов), так как чем меньше потеря мощности в них, тем меньше износ этих механизмов и тем менее вероятен выход их из строя («сгорание»).
На рис. 527 показаны графики расхода мощности при повороте танков с различными механизмами поворота.
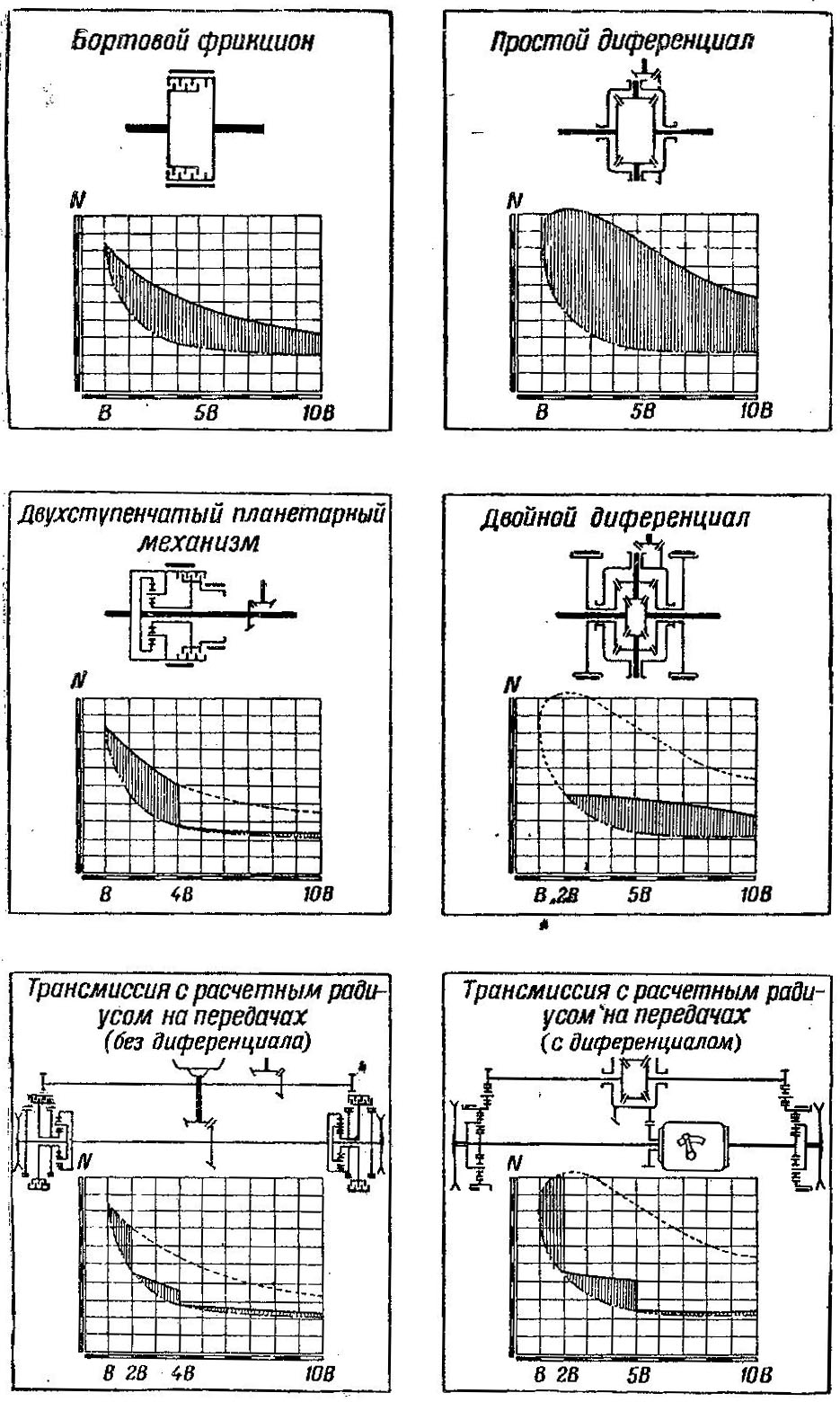
Рис. 527 Сравнительная оценка механизмов поворота
Разумеется, расход мощности для сравниваемых механизмов подсчитан в предположении одинаковых условий их работы, т.е. рассматривался поворот танков равного веса на одном и том же грунте и при одной и той же угловой скорости. На нижней кривой каждого графика показана мощность внешних сопротивлений, она одинакова для всех механизмов. Верхняя кривая показывает изменение потребной мощности. Заштрихованная часть диаграммы показывает тормозную мощность.
Из графиков видно, что двухступенчатый планетарный механизм обеспечивает весьма значительную экономию мощности по сравнению с бортовым фрикционом. Более сложная трансмиссия с двойным подводом мощности позволяет еще несколько снизить потери мощности, но лишь в весьма узком интервале малых радиусов поворота, что мало скажется на общем расходе мощности.
Все дифференциальные механизмы, сохраняющие при повороте среднюю скорость v0постоянной, обусловливают большие потери мощности в сравнении с независимыми механизмами. Наибольшие потери дает простой дифференциал — самый неэкономичный из всех механизмов поворота. Потеря мощности при поворотах танка с двойным дифференциалом несколько выше, чем с независимым механизмом (двухступенчатым планетарным) в том случае, когда оба механизма имеют одинаковые расчетные радиусы.
На графиках не приведен расход мощности танков с трансмиссиями, обеспечивающими непрерывное изменение радиуса поворота без потери мощности в тормозах (гидравлическая при двойном подводе мощности, электрическая). Мощность двигателя, потребная в этом случае, будет равна мощности внешних сопротивлений (нижняя кривая). Практически же, как мы отмечали, и при этих трансмиссиях в ряде случаев не удается избежать потерь мощности в тормозах или реостатах.
С точки зрения устойчивости поворота некоторое преимущество имеют трансмиссии с двойным подводом мощности; при этом чем больше передач в коробке, тем выше устойчивость поворота.
Существенное значение для оценки механизма имеет простота его устройства, ухода за ним, регулировки и надежность в работе. Так, применение двойного дифференциала в известной мере оправдывается именно этими его качествами. Но нельзя забывать об ухудшении маневренности танка, связанной с большой величиной расчетного радиуса поворота. Точно так же сравнительная простота устройства бортовых фрикционов далеко не всегда искупает большой расход мощности и недостаточную надежность. Поэтому механизмы поворота (как и всякие другие) надо сравнивать не по отдельным показателям, а в целом, по их совокупности, учитывая также и особенности танка, на котором они установлены (вес, удельную мощность, устройство коробки передач, тип приводов управления и т. д.).


